Abstrak
Proyeksi perubahan muka air laut regional dalam berbagai skenario perubahan iklim biasanya melibatkan simulasi lanjutan dari respons gravitasi, rotasi, dan deformasi (GRD) Bumi terhadap perubahan massa es, yang memerlukan biaya komputasi yang besar jika diterapkan pada kerangka kerja probabilistik yang memerlukan ribuan hingga jutaan sampel. Di sini kami membangun emulator perubahan muka air laut regional di 27 lokasi pesisir, karena efek GRD yang terkait dengan perubahan massa Lapisan Es Antartika di masa mendatang selama abad ke-21. Emulator dievaluasi terhadap model muka air laut numerik yang diterapkan pada kumpulan simulasi model lapisan es Lapisan Es Antartika hingga tahun 2100. Kami membangun emulator berbasis fisika menggunakan pendekatan kernel sensitivitas terkini dan membandingkannya dengan emulator berbasis pembelajaran mesin (metode jaringan saraf dan autoencoder variasional bersyarat). Untuk mengukur ketidakpastian, kami memperoleh interval prediksi yang dikalibrasi dengan baik untuk perubahan muka air laut regional melalui inferensi konformal terpisah dan regresi linier, dan menunjukkan bahwa putusan Monte Carlo tidak menghasilkan ketidakpastian yang dikalibrasi dengan baik dalam hal ini. Kami juga menunjukkan peningkatan signifikan dalam efisiensi komputasi menggunakan emulator berbasis fisika dan jaringan saraf dibandingkan dengan model numerik untuk solusi permukaan laut regional yang lengkap. Secara keseluruhan, kami menemukan emulator berbasis fisika sedikit mengungguli emulator pembelajaran mesin untuk masalah ini.
Poin-poin Utama
- Kami membandingkan metode berbasis kernel dan jaringan saraf untuk meniru perubahan permukaan laut regional dari simulasi perubahan massa Lapisan Es Antartika
- Kami menemukan bahwa metode kernel adalah yang paling akurat dan semua metode memberikan percepatan yang substansial
- Kami mengukur ketidakpastian dalam prediksi emulator menggunakan inferensi konformal terpisah dan regresi linier
Ringkasan Bahasa Sederhana
Perubahan permukaan laut bervariasi secara regional karena perubahan berat lapisan es dan gletser merusak kerak Bumi dan mengubah medan gravitasi Bumi serta sumbu rotasinya. Sementara model permukaan laut numerik digunakan secara luas untuk memproyeksikan perubahan permukaan laut akibat efek ini, model tersebut memerlukan ribuan evaluasi untuk mengukur ketidakpastian dalam proyeksi. Untuk mempercepat proses ini, kami mengevaluasi kelayakan berbagai model sederhana yang mengorbankan sebagian akurasi demi percepatan komputasi yang substansial. Kami mempertimbangkan metode pembelajaran mesin dan pendekatan fisika tereduksi serta menerapkan “emulator” ini ke 27 lokasi pesisir utama. Emulator menunjukkan akurasi prediksi yang tinggi dan berjalan antara 160 dan 240 kali lebih cepat daripada model permukaan laut numerik. Kami kemudian mengukur ketidakpastian dalam perubahan permukaan laut regional yang disebabkan oleh emulator itu sendiri menggunakan dua teknik. Berdasarkan hal ini, kami menemukan bahwa pendekatan fisika tereduksi adalah yang paling akurat, cepat dievaluasi, mudah dibuat, dan menghasilkan ketidakpastian yang akurat jika digabungkan dengan teknik kuantifikasi ketidakpastian yang disebutkan di atas.
1 Pendahuluan
Masyarakat dan infrastruktur pesisir berada di bawah ancaman serius dari kenaikan muka air laut yang disebabkan oleh perubahan iklim (Fox-Kemper et al., 2021 ; Hauer et al., 2020 ). Rata-rata muka air laut global (GMSL) naik sebesar 0,20 m selama seabad terakhir, dan laporan penilaian Panel Antarpemerintah tentang Perubahan Iklim terbaru (Fox-Kemper et al. ( 2021 )) mengindikasikan bahwa “hampir pasti” bahwa GMSL akan terus naik hingga tahun 2100. Kenaikan muka air laut yang berkelanjutan diperkirakan terjadi terlepas dari skenario emisi gas rumah kaca antropogenik karena kemungkinan semua proses utama berkontribusi pada GMSL yang terus beroperasi. Perubahan muka air laut bervariasi secara spasial, dan muka air laut relatif (RSL, yaitu, ketebalan lautan) dapat berbeda hingga faktor dua relatif terhadap GMSL di seluruh wilayah dunia (Fox-Kemper et al., 2021 ; Kopp et al., 2015 ). Variasi dalam RSL disebabkan oleh efek sterik (perubahan dalam kepadatan dan salinitas laut) dan perubahan permukaan laut yang dinamis, serta efek gravitasi, rotasi, dan deformasi (GRD) (Fox-Kemper et al., 2021 ; Gregory et al., 2019 ; Hamlington et al., 2020 ; Kopp et al., 2015 ; Slangen et al., 2014 ). Tidak seperti dua faktor lainnya, efek GRD disebabkan oleh perubahan dalam pemuatan massa permukaan seperti lapisan es dan laut, gletser, dan penyimpanan air terestrial (waduk, danau, air tanah). Artinya, redistribusi massa di permukaan Bumi merusak Bumi yang padat, mengganggu medan gravitasi Bumi, dan menggeser sumbu rotasi Bumi. Selain itu, Bumi yang padat mengalami deformasi seiring waktu sebagai respons terhadap perubahan beban permukaan. Proses kompleks ini menghasilkan perubahan permukaan laut yang bervariasi secara spasial dan temporal yang disebut sebagai “sidik jari permukaan laut” yang unik pada geometri perubahan massa es (Farrell & Clark, 1976 ; Mitrovica et al., 2011 ).
Ketidakpastian dalam perubahan permukaan laut di masa depan didominasi oleh perubahan pada Lapisan Es Antartika (AIS) (Bakker et al., 2017 ; Edwards et al., 2021 ; Fox-Kemper et al., 2021 ; Kopp et al., 2017 ), karena lapisan ini mengandung sektor-sektor besar yang esnya terdampar di bawah permukaan laut dan berpotensi rentan terhadap penyusutan cepat melalui ketidakstabilan lapisan es laut (Schoof, 2007 ). Proyeksi kontribusi AIS di masa mendatang terhadap permukaan laut membaik melalui upaya perbandingan model komunitas yang terkoordinasi (Edwards et al., 2021 ; Nowicki et al., 2020 ; Seroussi et al., 2020 ), serta ansambel besar simulasi AIS dari model tunggal yang mengukur ketidakpastian (Berdahl et al., 2023 ; Bulthuis et al., 2019 ; Coulon et al., 2024 ). Studi-studi ini mengindikasikan berbagai kemungkinan hasil masa depan untuk AIS hingga tahun 2100 dan seterusnya. Lebih jauh, studi-studi terkini telah menunjukkan bahwa geometri variabel dari perubahan massa AIS yang diproyeksikan memiliki dampak signifikan pada RSL mendatang akibat efek GRD (Cederberg et al., 2023 ; Roffman et al., 2023 ).
Karena perubahan permukaan laut memiliki ketidakpastian yang besar dan juga bervariasi secara regional, proyeksi probabilistik RSL di kota-kota yang menjadi perhatian yang menggabungkan seluruh rentang proyeksi AIS sangat penting untuk menilai dampak dan risiko iklim di masa mendatang. Kumpulan proyeksi lapisan es ini telah digunakan dalam kerangka kerja probabilistik untuk menganalisis RSL yang menggunakan pengambilan sampel Monte Carlo dengan sejumlah besar evaluasi (urutanmathematical equation) untuk menghasilkan fungsi distribusi probabilitas permukaan laut regional di masing-masing kota yang diminati (Jevrejeva et al., 2018 ; Kopp et al., 2023 ). Namun, kerangka kerja ini sejauh ini mengasumsikan sidik jari permukaan laut statis yang dihitung dengan hanya memperhitungkan perubahan ketebalan es total untuk setiap lapisan es dan wilayah gletser (Kopp et al., 2023 ). Proyeksi ini akan ditingkatkan dengan mempertimbangkan sidik jari permukaan laut yang berkembang secara temporal. Karena kerangka kerja perubahan permukaan laut probabilistik memerlukan evaluasi puluhan ribu sampel (Kopp et al., 2023 ; Wong et al., 2017 ), mereka biasanya bergantung pada emulator atau parameterisasi model dan proses kompleks yang cepat dievaluasi yang mencakup trade-off yang dapat diterima antara akurasi dan biaya komputasi. Tujuan kami dalam pekerjaan ini adalah untuk mengevaluasi dua metode untuk memperkenalkan sidik jari permukaan laut spesifik sampel ke dalam kerangka kerja probabilistik yang menghasilkan distribusi RSL untuk kota-kota individual: emulasi model permukaan laut menggunakan (a) pembelajaran mesin, dan (b) kernel sensitivitas (Al-Attar et al., 2024 ) yang diturunkan dari metode adjoint untuk versi sederhana dari model permukaan laut.
Emulator adalah model pengganti yang meniru simulator yang mendasarinya (seperti model permukaan laut dalam studi ini) dan efisien secara komputasi, berfungsi sebagai alternatif untuk model yang direplikasinya. Pentingnya emulator menjadi sangat jelas ketika simulator terlalu mahal secara komputasi dan ketika emulator dapat secara efektif mengukur ketidakpastian. Karena hubungan yang kompleks antara perubahan beban massa dan sidik jari permukaan laut (Cederberg et al., 2023 ; Mitrovica et al., 2011 ; Roffman et al., 2023 ) dan biaya penghitungan sidik jari permukaan laut yang berkembang seiring waktu menggunakan model permukaan laut, pembelajaran mesin (ML) menyediakan satu jalan yang menjanjikan untuk membuat emulator sidik jari permukaan laut yang murah secara komputasi yang dievaluasi di lokasi yang diinginkan.
Pada dasarnya, ML mengacu pada berbagai pendekatan komputasi untuk memperkirakan fungsi dasar yang merangkum hubungan input-output. Pekerjaan terkini telah menunjukkan potensi jaringan saraf konvolusional sferis berbasis grafik untuk meniru model permukaan laut yang diterapkan pada penyesuaian isostatik glasial zaman es selama deglasiasi terakhir dan mencapai 100–1.000mathematical equationpercepatan (Lin et al., 2023 ). Studi lain menggunakan jaringan saraf tiruan untuk mengembangkan emulator untuk efek variasi lateral dalam struktur reologi Bumi yang sering kali ditinggalkan dari model permukaan laut (Love et al., 2023 ). ML juga telah diterapkan pada proyeksi model lapisan es yang membentuk masukan untuk model permukaan laut. Van Katwyk et al. ( 2023 ) membuat emulator untuk kontribusi dari AIS ke GMSL dengan melatih jaringan saraf pada ansambel eksperimen model lapisan es. Rohmer et al. ( 2022 ) menggunakan ansambel serupa, dalam kasus ini untuk Lapisan Es Greenland, bersama dengan pendekatan atribusi berbasis ML untuk mengukur pengaruh keputusan pemodelan lapisan es yang berbeda terhadap proyeksi kontribusi lapisan es di masa mendatang terhadap GMSL. Metode ML juga telah digunakan untuk memprediksi sinyal muka air laut regional yang kompleks dari kumpulan data perubahan muka air laut historis yang diamati pada skala waktu bulan ke tahun (misalnya, Altunkaynak & Kartal, 2021 ; Ayinde et al., 2023 ; Guillou & Chapalain, 2021 ; Nieves et al., 2021 ; Song et al., 2021 ; Tur et al., 2021 ) dan diterapkan pada berbagai komponen individual model lapisan es (misalnya, Brinkerhoff et al., 2021 ; He et al., 2023 ; Jouvet, 2023 ; Jouvet et al., 2022 ; Riel & Minchew, 2023 ; Riel et al., 2021 ; Rosier et al., 2023 ; Verjans & Robel, 2024 ). Namun, penggunaan ML untuk mempercepat proyeksi probabilistik perhitungan permukaan laut regional untuk masing-masing kota belum dicoba. Dari karya yang ada, emulasi model permukaan laut Lin et al. ( 2023 ) adalah analog yang paling dekat, tetapi di sini kami memilih untuk fokus pada masalah yang lebih sederhana yang tidak bergantung pada waktu untuk proyeksi jangka pendek dengan sejumlah kecil lokasi target, dibandingkan dengan masalah yang lebih kompleks yang bergantung pada waktu dan spasial yang ditangani oleh Lin et al. ( 2023 ).
Pendekatan kedua yang kami evaluasi menggunakan kernel sensitivitas untuk setiap lokasi yang diminati (kota) yang dengannya bidang perubahan massa es dapat dikalikan untuk memperoleh RSL untuk lokasi tersebut tanpa perlu menyelesaikan ulang persamaan permukaan laut (Al-Attar et al., 2024 ). Pendekatan kernel sensitivitas mengeksploitasi teorema resiprositas yang baru-baru ini ditetapkan untuk persamaan permukaan laut elastis yang menunjukkan bahwa RSL di satu lokasi karena perubahan beban massa (misalnya, dari lapisan es) di lokasi lain adalah sama jika titik evaluasi pemuatan dan RSL dibalik (Al-Attar et al., 2024 ). Pendekatan kernel memerlukan beberapa asumsi pembatas minor (reologi elastis; garis pantai tetap, termasuk garis dasar lapisan es; ketidakmampuan untuk mengevaluasi kondisi flotasi lapisan es secara konsisten) yang diterapkan pada persamaan permukaan laut dan harus dihitung secara terpisah untuk setiap lokasi yang diminati. Pembatasan ini memotivasi perbandingan dengan emulasi ML sebagai alternatif potensial.
Dalam studi ini, kami membandingkan pendekatan emulasi ML jaringan saraf dengan pendekatan sensitivitas kernel untuk tujuan evaluasi cepat banyak sampel di sejumlah lokasi geografis yang sederhana. Kami mengembangkan beberapa emulator ML jaringan saraf untuk pemecah persamaan permukaan laut yang mapan dari HK Han et al. ( 2022 ) untuk memprediksi perubahan RSL yang disebabkan oleh perubahan massa AIS. Emulator dilatih pada serangkaian simulasi model permukaan laut yang dipaksakan dengan ansambel terbaru proyeksi model lapisan es AIS hingga 2100 (ISMIP6, Serousi et al., 2020 ). Karena kami berfokus pada metode untuk menghasilkan distribusi RSL untuk kota-kota individual, kami melatih emulator untuk mempertimbangkan lokasi 27 kota pesisir utama; perhatikan bahwa emulator jaringan saraf secara bersama-sama memprediksi perubahan RSL untuk semua 27 kota sekaligus, sedangkan pendekatan sensitivitas kernel memiliki kernel yang berbeda untuk masing-masing dari 27 lokasi. Kami mulai dengan membandingkan berbagai emulator berbasis jaringan saraf, serta metode sensitivitas kernel, dan mengevaluasi kekuatan dan kelemahan mereka untuk aplikasi ini. Kami kemudian mengukur ketidakpastian dalam prediksi emulator dengan menghasilkan interval prediksi menggunakan inferensi split-conformal (Lei et al., 2018 ) dan regresi linier sederhana, metode yang telah digunakan untuk mengkalibrasi model peramalan numerik (HR Glahn & Lowry, 1972 ; B. Glahn et al., 2009 ; Lovegrove & Siegert, 2023 ). Kami juga membandingkan Monte Carlo dropout (Srivastava et al., 2014 ), metode yang umum digunakan untuk kuantifikasi ketidakpastian dalam jaringan saraf. Selanjutnya, kami menerapkan emulator untuk menghasilkan proyeksi probabilistik perubahan RSL yang disebabkan oleh perubahan massa AIS dengan menghasilkan ansambel proyeksi lapisan es buatan. Akhirnya, kami menilai biaya relatif dan akurasi pendekatan emulasi ML dan sensitivitas kernel untuk aplikasi ini.
2 Deskripsi Data
Pelatihan emulator ML memerlukan kumpulan data simulasi proyeksi perubahan massa lapisan es dan sidik jari permukaan laut regional yang sesuai, yang dibagi menjadi kelompok pelatihan, validasi, dan pengujian. Bagian berikut menjelaskan pembuatan kumpulan data ini secara terperinci.
2.1 Kumpulan Data Perubahan Massa Lapisan Es
Set data input untuk alur kerja kami adalah himpunan perubahan massa AIS masa depan yang dihitung (yaitu, disimulasikan) oleh model lapisan es. Untuk ini, kami mengadopsi hasil eksperimen AIS dari Ice Sheet Model Intercomparison Project for Coupled Model Intercomparison Project Phase 6 (ISMIP6) (Seroussi et al., 2020 ). Protokol ISMIP6-Antartika menetapkan konfigurasi eksperimen standar untuk model lapisan es untuk menghasilkan proyeksi AIS dari tahun 2015 hingga 2100 (Nowicki et al., 2020 ). Simulasi model lapisan es dipaksa oleh atmosfer dan keluaran laut dari enam model iklim Coupled Model Intercomparison Project Phase 5 (CMIP5) yang berbeda untuk skenario emisi gas rumah kaca tinggi RCP8.5 dan dua model iklim untuk skenario emisi rendah RCP2.6. Selain menguji berbagai pemaksaan iklim, berbagai eksperimen menguji representasi yang berbeda dari pencairan dasar lapisan es dan potensi penghilangan wilayah lapisan es melalui hidrofraktur. Secara total, ada 21 eksperimen yang ditetapkan; di sini kami memilih delapan eksperimen yang protokol standarnya ditentukan. Eksperimen tersebut dijalankan oleh 13 kelompok pemodelan di seluruh dunia, dan hasilnya dianalisis pada kisi referensi umum. Setiap kelompok pemodelan juga melakukan uji coba kontrol hingga 2100 menggunakan pemaksaan iklim konstan yang stabil untuk mengukur pergeseran model. Kumpulan tersebut mewakili berbagai macam kompleksitas model lapisan es, resolusi kisi, dan karakteristik model. Khususnya, tidak ada model lapisan es dalam kumpulan ISMIP6 yang menyertakan efek GRD.
Untuk menyiapkan data proyeksi lapisan es ini sebagai input ke model permukaan laut, kami melakukan sejumlah langkah pemrosesan. Pertama, kami menghitung perubahan dalam bidang spasial ISMIP6 “land_ice_thickness” dari nilai awalnya. Karena ada pergeseran besar dalam uji coba kontrol banyak simulasi (Aschwanden et al., 2021 ), kami menghapus perubahan ketebalan dalam uji coba kontrol untuk setiap model dari setiap proyeksi, seperti yang dilakukan dalam analisis ISMIP6 (Seroussi et al., 2020 ). Langkah ini sangat penting untuk pemodelan perubahan permukaan laut regional, karena beberapa bagian dari perubahan ketebalan es dari proyeksi mentah akan terkait dengan bias yang melekat pada setiap model lapisan es (yaitu, pergeseran model), yang tidak ingin kami masukkan ke dalam kalkulasi sidik jari permukaan laut kami. Sementara keluaran ISMIP6 diposting setiap tahun, kami melakukan subsampel ke interval 5 tahun karena perubahan tahunan relatif kecil, yang mengarah ke 17 tingkat waktu perubahan ketebalan es. Terakhir, kami memetakan ulang bidang perubahan ketebalan es dari proyeksi stereografi kutub 8 km kemathematical equationkisi Gaussian lintang/bujur yang digunakan oleh model permukaan laut menggunakan metode pemetaan ulang konservatif untuk memastikan total perubahan massa AIS tidak berubah oleh pemetaan ulang.
Sebanyak 194 proyeksi AIS dihasilkan untuk ISMIP6 di berbagai eksperimen dan model yang digunakan, dan di sini kami membatasi diri pada 71 proyeksi yang berasal dari delapan eksperimen dengan protokol standar (eksperimen 5–10 dan 11–12), menghilangkan sejumlah kecil proyeksi karena kesalahan pemrosesan yang terkait dengan masalah dengan konvensi format data. Dengan memperhitungkan 17 level waktu yang dipertahankan untuk setiap proyeksi, kami memiliki total 1.207 bidang perubahan ketebalan es dalam set data masukan kami yang digunakan untuk pelatihan, validasi, dan pengujian emulator ML.
2.2 Kumpulan Data Permukaan Laut: Perhitungan Sidik Jari Permukaan Laut
Kami menghasilkan sidik jari permukaan laut yang terkait dengan berbagai pola kehilangan massa AIS menggunakan model permukaan laut yang dijelaskan oleh HK Han et al. ( 2022 ), versi terbaru dari model permukaan laut yang dijelaskan dalam Kendall et al. ( 2005 ) dan Gomez et al. ( 2010 ). Model tersebut menghitung perubahan permukaan laut barista dan efek GRD terkait yang disebabkan oleh perubahan massa es daratan dengan memecahkan persamaan permukaan laut statis (Farrell & Clark, 1976 ; Mitrovica & Milne, 2003 ) menggunakan algoritma pseudo-spektral yang dijelaskan secara rinci dalam Kendall et al. ( 2005 ), dengan pemotongan hingga derajat harmonik bulat dan orde 512. Kerangka permukaan laut memperhitungkan migrasi garis pantai (Milne & Mitrovica, 1998 ), termasuk penggenangan cekungan laut yang saat ini tertutup gletser seiring dengan surutnya lapisan es yang terdampar, serta gangguan pada sumbu rotasi Bumi (Mitrovica & Milne, 2003 ; Mitrovica et al., 2005 ). Simulasi kami mencakup pemeriksaan es yang mengapung dengan mengevaluasi kriteria flotasi secara iteratif saat RSL diselesaikan. Kriteria flotasi mengasumsikan kepadatan es sebesar 910 kgmathematical equationdan kepadatan air (pencairan es dan lautan) sebesar 1.000 kgmathematical equationPerlu dicatat bahwa karena kami tertarik pada proyeksi perubahan permukaan laut di masa depan, tidak ada data observasi untuk mengevaluasi perhitungan perubahan permukaan laut kami dan kami berasumsi bahwa perhitungan oleh model HK Han et al. ( 2022 ) cukup akurat.
Selain pola proyeksi hilangnya massa es AIS, simulasi memerlukan model untuk struktur reologi Bumi padat. Kami mengadopsi model elastis simetri radial untuk Bumi dengan sifat elastis dan kepadatan yang berasal dari model PREM seismik (Dziewonski & Anderson, 1981 ). Kami juga mengevaluasi simulasi dengan struktur Bumi viskoelastis menggunakan viskositas Bumi yang bervariasi terhadap kedalaman yang diberikan oleh profil viskositas VM7 (Roy & Peltier, 2017 , 2018 ). Untuk jangka waktu 85 tahun dari eksperimen ISMIP6, kontribusi dari deformasi viskos dapat diabaikan. Kami mencatat bahwa nilai viskositas ini mewakili rata-rata global; meskipun sesuai untuk Antartika Timur dan 27 lokasi pesisir jauh kami, struktur Bumi ini tidak secara akurat menangkap struktur Bumi di Antartika Barat di mana viskositas mantel atas dianggap 2–3 orde besaran lebih rendah dari rata-rata global (Barletta et al., 2018 ; Nield et al., 2014 ). Kami mencatat bahwa sementara sudah mapan bahwa struktur Bumi di Antartika menunjukkan heterogenitas lateral yang kuat (Lloyd et al., 2023 ) yang mungkin berdampak pada proyeksi perubahan permukaan laut lokal, sensitivitas permukaan laut jauh terhadap struktur Bumi 1D versus 3D hanya menjadi cukup besar untuk dipertimbangkan dalam proyeksi skala jangka panjang (multi-centennial atau lebih lama) (Pan et al., 2021 ; Powell et al., 2022 ), yang berada di luar skala waktu yang kami pertimbangkan dalam pekerjaan ini. Kami melakukan uji sensitivitas tambahan menggunakan viskositas mantel yang lebih rendah yang sesuai untuk Antartika Barat dan mengonfirmasi bahwa hasilnya hanya berbeda beberapa persen dari konfigurasi Bumi elastis di luar Antartika untuk simulasi 85 tahun ini, yang membenarkan penggunaan struktur Bumi elastis saja.
Karena model permukaan laut berjalan pada grid global tetapi set data ISMIP6-AIS asli disediakan pada grid lokal, kami mengadopsi topografi dari set data ETOPO2 (NOAA National Centers for Environmental Information, 2022 ) untuk wilayah di luar domain model lapisan es. Dengan rangkaian waktu perubahan ketebalan lapisan es yang telah diproses sebelumnya dan struktur Bumi yang dijelaskan di atas, kami melakukan serangkaian simulasi permukaan laut dengan interval waktu 5 tahun dan menghasilkan set data keluaran perubahan permukaan laut untuk pelatihan, validasi, dan pengujian emulator. Contoh peta perubahan permukaan laut yang terkait dengan perubahan ketebalan AIS diilustrasikan dalam Gambar 1. Perhatikan bahwa sementara 17 tingkat waktu yang dievaluasi berurutan dalam waktu, efek GRD elastis yang dipertimbangkan bersifat sesaat dan tidak ada ketergantungan waktu dalam solusi model. Artinya, medan RSL dihitung dari medan perubahan ketebalan es yang diberikan tanpa ketergantungan pada riwayat perubahan ketebalan es.
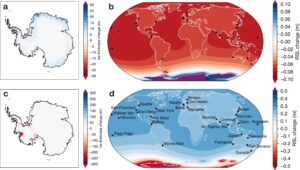
Awalnya kami mencoba meniru keseluruhanmathematical equationruang keluaran dimensi model permukaan laut (per langkah waktu), dengan model berkinerja terbaik menggunakan autoencoder (Kramer, 1991 ) untuk reduksi dimensi pada input dan output dan jaringan saraf umpan maju yang menghubungkan antara ruang dimensi tereduksi. Hasil awal kami sangat bervariasi dalam kualitas—sementara beberapa dari seluruh bidang dalam set pengujian dapat ditiru dengan andal, sekitar 10% dari bidang pengujian global ditiru dengan buruk (kesalahan akar kuadrat rata-rata yang dinormalisasi melebihi 0,11). Selain itu, koordinat lintang-bujur dari keluaran spasial model permukaan laut menambah kompleksitas dalam merepresentasikan permukaan bola secara akurat dalam dua dimensi (Lin et al., 2023 ). Mengingat tujuan utama kami untuk meniru RSL di serangkaian kota terpilih, bidang RSL global tidak sepenuhnya diperlukan. Oleh karena itu, untuk meningkatkan akurasi emulator ML, kami memilih untuk hanya mengevaluasi perubahan RSL di 27 lokasi pengukur pasang surut jangka panjang yang diidentifikasi oleh Meyssignac et al. ( 2017 ) (Gambar 1c ), yang berasal dari Layanan Permanen untuk Permukaan Laut Rata-rata (Holgate et al., 2013 ).
2.3 Pembagian Data Pelatihan, Validasi, dan Uji
Seluruh set data bidang perubahan massa AIS ISMIP6, beserta keluaran perubahan permukaan laut yang dipecahkan secara numerik, dibagi menjadi set data pelatihan, validasi, dan uji, seperti yang umum dilakukan dalam ML (Hastie et al. ( 2009 )), dengan 80% digunakan untuk pelatihan, 10% digunakan untuk validasi, dan 10% digunakan untuk set uji hold-out. Seperti disebutkan di atas, ini merupakan 1.207 pasang bidang perubahan massa AIS dan perubahan permukaan laut relatif global di berbagai model lapisan es, eksperimen, dan tingkat waktu.
Untuk memastikan representasi setiap tahun di tiga pemisahan data, pasangan data input-output dari 71 simulasi lapisan es per tahun dipilih secara acak untuk berada dalam set pelatihan, validasi, dan pengujian; yaitu, kami melakukan stratifikasi berdasarkan tahun saat menyusun pemisahan pelatihan, validasi, dan pengujian. Dari total 71 simulasi lapisan es untuk tahun tertentu, 57 dipilih secara acak untuk berada dalam set pelatihan, tujuh dipilih secara acak untuk berada dalam set validasi, dan tujuh dipilih secara acak untuk berada dalam set pengujian, menghasilkan 80% untuk pelatihan, 10% untuk validasi, dan 10% untuk pengujian. Pemisahan data akhir terdiri dari 969 dalam pelatihan, 119 dalam validasi, dan 119 dalam pengujian, di mana input setiap pemisahan distandarisasi untuk memiliki rata-rata 0 dan varians unit. Panjang vektor masukan yang diratakan untuk setiap langkah waktu setiap simulasi adalah 579.121, dan vektor keluarannya adalah 27 lokasi pengukur pasang surut jangka panjang.
3 Model ML
Bahasa Indonesia: Kami membangun model pembelajaran mesin (ML) yang mengambil vektor perubahan ketebalan es di Antartika yang berasal dari simulasi ISMIP-6 sebagai input dan menghasilkan prediksi simulasi perubahan RSL yang dihasilkan di 27 lokasi pengukur pasang surut jangka panjang (Gambar 1c dan 1d ). Artinya, dalam emulator perubahan RSL kami, inputnya adalah vektor perubahan ketebalan es yang diratakan, dan outputnya adalah prediksi perubahan RSL yang dihasilkan untuk 27 lokasi pengukur pasang surut jangka panjang. Idealnya, model ML harus secara akurat memprediksi nilai perubahan RSL yang disimulasikan, secara komputasi lebih terjangkau daripada menjalankan simulasi numerik penuh, dan juga memungkinkan kuantifikasi ketidakpastian prediksi yang valid secara statistik. Berikut ini, kami menjelaskan implementasi ML jaringan saraf yang dibangun dan dibandingkan: jaringan saraf umpan maju (NN) dan autoencoder variasional bersyarat (CVAE). Kami memilih jaringan saraf karena prevalensinya dalam banyak implementasi ML modern yang banyak digunakan, termasuk transformer dalam model bahasa dan visi yang besar (Vaswani et al., 2017 ), untuk ML berbasis fisika (Raissi et al., 2019 ), dan dalam kecerdasan buatan generatif (Achiam et al., 2023 ). Kami membahas kemungkinan lain di akhir bagian ini.
3.1 Jaringan Syaraf Tiruan Umpan Maju (NN)
Jaringan saraf umpan maju (NN) merupakan komponen dasar dari jaringan saraf dalam. Tujuan utama NN adalah mempelajari (atau memperkirakan) pemetaanmathematical equationdari masukanmathematical equationuntuk mengeluarkanmathematical equation, dicapai melalui komposisi fungsi yang diatur oleh parametermathematical equationyang terdiri dari bobot dan istilah bias. Tugas perkiraan setara dengan menentukan estimasi terbaikmathematical equationyang meminimalkan fungsi kerugian (misalnya, kesalahan kuadrat rata-rata) menggunakan set pelatihan, yang biasanya diperbarui secara berulang dengan backpropagation (Rumelhart et al., 1986 ).
Rutin optimasi yang umum digunakan seperti stochastic gradient descent (SGD) (Bottou, 2010 ) dan ADAM (Kingma & Ba, 2017 ) untuk pemasangan jaringan neural adalah hal yang umum. Jaringan neural feedforward (NN) terdiri dari lapisan input,mathematical equationlapisan tersembunyi, dan lapisan keluaran, di manamathematical equationmenunjukkan jumlah lapisan tersembunyi.mathematical equationlapisan tersembunyi dilengkapi denganmathematical equationneuron, yang berfungsi sebagai dimensi keadaan tersembunyi.
Unit-unit lapisan (neuron) saling terhubung melalui transformasi linier dan fungsi aktivasi, yang dilambangkan sebagaimathematical equation, Di manamathematical equationBahasa Indonesia:mathematical equation, Danmathematical equationberkorespondensi dengan bobot, bias, dan fungsi aktivasi, secara berurutan. Urutan operasi ini di setiap lapisan dapat menghasilkan perkiraan berkualitas tinggi dari fungsi-fungsi kompleks. Potensi untuk perkiraan tersebut ditingkatkan oleh fungsi aktivasi, seperti unit linier terektifikasi (RELU), yang memperkenalkan non-linearitas. Selain kemampuan perkiraannya yang kaya, perangkat lunak yang mudah digunakan, seperti PyTorch oleh Paszke et al. ( 2019 ), telah berkontribusi pada popularitas NN. Untuk pengenalan NN yang lebih rinci, lihat Goodfellow et al. ( 2016 ).
Dalam implementasi kami, kami menggunakan arsitektur jaringan saraf yang terdiri darimathematical equationlapisan tersembunyi. Karena banyaknya lapisan, kami menganggap ini sebagai jaringan saraf dalam (Goodfellow et al., 2016 ). Kami menggunakan fungsi aktivasi RELU antara lapisan, sementara fungsi aktivasi linier diterapkan antara lapisan tersembunyi terakhir dan lapisan keluaran. Jumlah neuron dalam setiap lapisan adalahmathematical equation. Dengan menggunakan root mean squared error (RMSE) sebagai fungsi kerugian, kami melatih model dengan pengoptimal SGD dengan tingkat pembelajaran 0,001. Selama proses pelatihan, kami memantau konvergensi kerugian pada set validasi. Untuk mencegah overfitting, kami juga memperkenalkan dropout (Srivastava et al., 2014 ) dengan probabilitas 0,3 antar lapisan. Kami mengimplementasikan NN menggunakan Pytorch versi 2.0.1 dengan Python versi 3.9.12.
3.2 Autoencoder Variasi Bersyarat (CVAE)
CVAE adalah arsitektur jaringan saraf modern yang digunakan secara luas yang memasangkan encoder ke decoder, dengan lapisan perantara di antara keduanya mewakili ruang laten berdimensi lebih rendah. CVAE menarik dan dapat efektif dalam membangun model generatif (misalnya, model generatif molekuler (Lim et al., 2018 ) dan model generatif pembelajaran zero-shot (Mishra et al., 2018 )). Kami mempertimbangkan CVAE sebagai tambahan pada NN feed-forward untuk mencoba pendekatan generatif untuk emulator perubahan permukaan laut, karena dengan mengambil sampel dari ruang laten yang sesuai, seseorang dapat menghasilkan sampel prediksi untuk input tertentu sebagai lawan dari prediksi tunggal; memang pendekatan ini berfungsi sebagai pendahulu untuk pendekatan kecerdasan buatan (AI) generatif seperti model difusi (Ho et al., 2020 ).
Asal usul CVAE dapat ditelusuri kembali ke autoencoder (AE) (Kramer, 1991 ) dan variational autoencoder (VAE) (Kingma & Welling, 2013 ). Secara umum, AE dilatih untuk mereproduksi input asli, dengan demikian mempelajari representasi laten berdimensi-tereduksi yang menangkap banyak informasi dari data input berdimensi lebih tinggi. Meskipun arsitektur VAE mirip dengan AE, VAE mengasumsikan bahwa ruang laten berdimensi-tereduksi mengikuti distribusi tertentu, sering kali normal multivariat dengan mean 0 dan matriks kovariansi identitas. Keuntungan utama VAE dibandingkan AE adalah dapat berfungsi sebagai model generatif dengan mengambil sampel dari distribusi lapisan laten antara.
Meskipun CVAE dan VAE serupa, CVAE memiliki fitur tambahan: kemampuan untuk menginstruksikan model untuk memprediksi keluaran berdasarkan informasi kondisional. Intinya, prediksi untuk masukan baru ditentukan dengan menggabungkan hasil acak dari ruang laten dengan informasi kondisional, yang dalam pengaturan kami adalah vektor perubahan ketebalan es. Vektor yang digabungkan ini, yang menggabungkan informasi kondisional dengan informasi laten, dilewatkan melalui dekoder untuk membuat prediksi. Untuk representasi visual, lihat Gambar 2 ; rincian lebih lanjut dijelaskan dalam tutorial Doersch ( 2016 ).
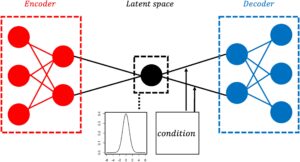
Implementasi CVAE kami untuk emulator perubahan permukaan laut mengambil seluruh vektor perubahan ketebalan es sebagai informasi bersyarat, menggabungkannya dengan penarikan laten, dan meneruskan vektor yang digabungkan melalui dekoder untuk membuat prediksi. Secara khusus, encoder terdiri darimathematical equationlapisan tersembunyi dengan neuron (mathematical equationBahasa Indonesia:mathematical equationBahasa Indonesia:mathematical equationBahasa Indonesia:mathematical equation) = (3.200, 1.600, 800, 400), dan menghasilkan 200 pasangan parameter (mathematical equationBahasa Indonesia:mathematical equation), Di manamathematical equationParameter ini sesuai dengan parameter distribusi lapisan antara posteriormathematical equation, yang diasumsikan mengikuti distribusi normal multivariat dengan vektor rata-ratamathematical equationdan matriks kovariansi diagonalmathematical equationKemudian, dekoder mengambil input berupa vektor gabungan dari vektor ketebalan lapisan es (yaitu, informasi kondisional) dan sampel yang ditransformasikan dari distribusi sebelumnya.mathematical equationuntuk lapisan antara. Dengan asumsimathematical equationmengikuti distribusi normal multivariat dengan mean 0 dan matriks kovariansi identitas, transformasi dicapai melalui reparametrisasimathematical equation(Kingma & Welling, 2013 ). Sama halnya dengan encoder, decoder juga terdiri darimathematical equationlapisan tersembunyi dengan jumlah neuron yang sama dengan encoder. Ia mengeluarkan prediksi perubahan permukaan laut di 27 lokasi pengukur pasang surut jangka panjang. Karena CVAE memprediksi nilai perubahan permukaan laut dan bukan merekonstruksi masukannya sendiri, ini merupakan modifikasi dari pendekatan AE yang biasa.
Fungsi kerugian yang digunakan untuk melatih adalah jumlah dari dua istilah: yang pertama adalah divergensi KL antara perkiraan variasi distribusi laten posteriormathematical equationdan distribusi sebelumnyamathematical equation, yang dapat dianggap sebagai penalti regularisasi. Yang kedua adalah istilah kesalahan kuadrat rata-rata untuk prediksi dari dekoder. Dalam implementasi kami, kami mengambil 500 sampel dari distribusi latenmathematical equationselama proses pembuatan prediksi, dan nilai prediksi akhir diperoleh dengan menghitung rata-rata dari 500 prediksi ini. CVAE diimplementasikan menggunakan PyTorch versi 2.0.1 dengan Python versi 3.9.17.
3.3 Opsi ML Lainnya
Kami mempertimbangkan model ML tambahan selain jaringan saraf sebagai perbandingan dasar. Perbandingan dasar ini adalah proses Gaussian stasioner dengan fungsi kovariansi eksponensial kuadrat (GP) dan hutan acak (RF). Dalam pekerjaan awal kami, kami menemukan bahwa emulator jaringan saraf bekerja sama akuratnya atau lebih akurat daripada garis dasar yang disebutkan sebelumnya. Selain itu, proses Gaussian dan emulator hutan acak menggunakan langkah pengurangan dimensionalitas tambahan untuk memungkinkan skalabilitas, sedangkan jaringan saraf mampu menangani input dimensi orde 100.000 tanpa prosedur pengurangan dimensi awal. Penggunaan pengurangan dimensionalitas dapat dilakukan dengan sejumlah cara (misalnya, komponen utama seperti yang kami terapkan atau proyeksi subruang acak), sehingga langkah pengurangan dimensi tambahan memperkenalkan faktor penggabungan dalam mengevaluasi kinerja model GP dan RF. Pertimbangan ini, ditambah dengan fakta bahwa jaringan saraf adalah model ML utama pilihan untuk aplikasi AI modern, membuat kami melanjutkan dengan hanya emulator jaringan saraf dalam membandingkan dengan metode sensitivitas kernel berbasis fisika, yang selanjutnya dijelaskan. Meskipun demikian , deskripsi dan tinjauan pendekatan GP dan RF disajikan dalam Lampiran A dan B.
4 Metode Sensitivitas Kernel
Meskipun aplikasi persamaan permukaan laut telah lama ditetapkan untuk memprediksi RSL yang disebabkan oleh perubahan tertentu dalam ketebalan es daratan (misalnya, Farrell & Clark, 1976 ; Kendall et al., 2005 ; Mitrovica & Milne, 2003 ), aplikasi tersebut memerlukan penyelesaian ulang persamaan permukaan laut untuk setiap pola spasial unik dari perubahan massa es daratan. Sebaliknya, dalam beberapa tahun terakhir, beberapa formulasi telah dibuat yang membalikkan hubungan antara perubahan massa es daratan dan RSL untuk menghasilkan peta sensitivitas RSL di lokasi tertentu terhadap pola spasial perubahan ketebalan es (Al-Attar et al., 2024 ; Crawford et al., 2018 ; Larour et al., 2017 ; Mitrovica et al., 2018 ). Pendekatan kernel sensitivitas ini menarik untuk masalah yang dibahas dalam studi ini untuk mengevaluasi banyak realisasi dampak perubahan ketebalan lapisan es pada RSL di sejumlah kecil lokasi pesisir; dengan menghitung kernel sensitivitas satu kali untuk setiap lokasi pesisir yang diminati, RSL di setiap lokasi akibat pola perubahan ketebalan lapisan es selanjutnya dapat dievaluasi dengan biaya komputasi perkalian vektor tunggal.
Dari metode kernel sensitivitas RSL yang telah dijelaskan, kami memilih metode terbaru Al-Attar et al. ( 2024 ) untuk aplikasi ini. Metode ini dibatasi pada masalah sidik jari elastis yang lebih sederhana yang kami pertimbangkan di sini, dengan mengabaikan kompleksitas kernel sensitivitas viskoelastis (lih. Crawford et al., 2018 ). Metode ini mencakup umpan balik rotasi yang penting untuk perubahan massa AIS (Cederberg et al., 2023 ; Roffman et al., 2023 ). Terakhir, metode ini mudah diimplementasikan dengan model sidik jari elastis apa pun dan tidak memerlukan diferensiasi otomatis atau implementasi model khusus.
Meskipun metode kernel sensitivitas menarik untuk aplikasi kita, metode ini mencakup beberapa penyederhanaan relatif terhadap model permukaan laut penuh yang digunakan. Selain keterbatasan reologi elastis, metode Al-Attar et al. ( 2024 ) memiliki keterbatasan yang mengharuskan posisi garis pantai tetap, yang menjadikan persamaan sidik jari elastis bersifat self-adjoint dan dengan demikian memungkinkan untuk menghasilkan kernel sensitivitas dengan model maju standar. Untuk perubahan permukaan laut (mathematical equationm) dari ensembel AIS ISMIP6 untuk 2015–2100, migrasi garis pantai akibat genangan air di wilayah pesisir diperkirakan dapat diabaikan. Namun, migrasi garis pantai akibat surutnya lapisan es laut yang terdampar tidak akan terjadi, dan harus ditangani secara kira-kira dalam model garis pantai tetap. Perbedaan antara model HK Han et al. ( 2022 ) dan Al-Attar et al. ( 2024 ) adalah bahwa model HK Han et al. ( 2022 ) mempertimbangkan ketebalan es penuh dari lapisan es laut dan mengevaluasi kondisi pengapungan secara berulang sebagai bagian dari solusi RSL. Selain itu, model ini memiliki topeng samudra yang berevolusi yang menyesuaikan saat es yang terdampar surut dari atau maju ke dalam sel grid, yang memungkinkan sel grid untuk secara dinamis beralih antara ditempati oleh es atau lautan (seperti yang dijelaskan dalam Kendall et al. ( 2005 )).
Kami menerapkan metode kernel sensitivitas Al-Attar et al. ( 2024 ) pada kode permukaan laut Al-Attar ( 2023 ), karena metode ini tidak sesuai dengan kemampuan garis pantai yang terus berkembang dari model Han. Kami memverifikasi kode tersebut dalam dua langkah: (a) Dengan menggunakan parameter model dan topografi yang sama serta perubahan ketebalan lapisan es, kami mengonfirmasi bahwa perbedaan RSL antara model HK Han et al. ( 2022 ) dan Al-Attar ( 2023 ) kecil (mathematical equationm) untuk solusi model maju; (b) Kami mengkonfirmasi bahwa perbedaan RSL antara solusi model maju dan metode kernel sensitivitas dengan kode Al-Attar ( 2023 ) sangat kecil (mathematical equationm), sebagaimana dilaporkan oleh Al-Attar et al. ( 2024 ). Meskipun kami tidak mengembangkan lebih lanjut metode kernel sensitivitas dalam karya ini, ini adalah aplikasi sistematis pertama yang kami ketahui untuk proyeksi masa depan perubahan permukaan laut yang disebabkan oleh Lapisan Es Antartika.
Untuk menghasilkan kernel sensitivitas, kami mengikuti prosedur Al-Attar et al. ( 2024 ). Pertama, kami menyiapkan set data referensi topografi awal dan ketebalan es. Karena setiap kelompok pemodelan ISMIP6 bebas untuk mengadopsi kondisi awal yang berbeda, kami menghitung topografi rata-rata dan ketebalan es di semua model. Selain itu, kami menghitung masker es untuk metode kernel yang mewakili penyatuan es dasar awal di semua model ISMIP6; ini memastikan bahwa perubahan ketebalan es dasar dari salah satu model ISMIP6 diperlakukan sebagai perubahan beban saat diterapkan pada metode kernel, sambil menghasilkan area lautan yang kira-kira sesuai untuk luasan es awal dari semua model. Dengan bidang ini, kami menghitung kernel sensitivitas untuk masing-masing dari 27 kota pesisir yang diinginkan, dengan menerapkan beban titik yang dihaluskan pada skala panjang karakteristik 1° seperti yang dijelaskan oleh Al-Attar et al. ( 2024 ). Untuk kemudian menerapkan kernel sensitivitas, kami mengintegrasikan kernel sensitivitas untuk setiap kota terhadap perubahan ketebalan es yang ditentukan. Untuk memperhitungkan asumsi garis pantai tetap, kami membatasi perubahan ketebalan es pada perubahan ketinggian di atas flotasi, perbedaan dari bagaimana perubahan ketebalan es diterapkan pada model HK Han et al. Perhatikan bahwa meskipun teori metode kernel sensitivitas menunjukkan bahwa metode tersebut akan memiliki akurasi yang sama dengan solusi sidik jari elastis garis pantai tetap (Al-Attar et al., 2024 ), serangkaian penyesuaian kecil dari aplikasi model HK Han et al. ( 2022 ) yang lebih kompleks (garis pantai tetap, membatasi perubahan beban pada ketinggian di atas flotasi, asumsi kondisi awal tunggal dan area laut) memperkenalkan kesalahan, yang sebagian memotivasi perbandingan terhadap metode ML yang dijelaskan di atas.
5 Kuantifikasi Ketidakpastian
Kami menyusun interval prediksi untuk nilai perubahan permukaan laut yang disimulasikan sebagai sarana untuk mengukur ketidakpastian emulator di 27 lokasi pengukur pasang surut jangka panjang. Kami mempertimbangkan tiga cara utama untuk mengukur ketidakpastian dalam studi ini: (a) pasca-pemrosesan regresi linier, (b) inferensi konformal terpisah, dan (c) putus Monte Carlo dengan pengambilan sampel variabel laten. Kami menjelaskan secara lebih rinci ketiga cara untuk mengukur ketidakpastian (UQ) di bawah ini, dan kami menekankan bahwa penggunaan UQ untuk pendekatan kernel sensitivitas merupakan kontribusi baru bagi literatur.
5.1 Interval Prediksi Regresi Linier
Seperti yang diulas dalam Lovegrove dan Siegert ( 2023 ), metode regresi linier telah digunakan untuk melakukan pascaproses keluaran dari prakiraan numerik dengan menggunakan keluaran model numerik sebagai variabel masukan (yaitu, kovariat) untuk regresi linier sederhana atau ganda, kasus terakhir ketika ada beberapa kovariat. Dalam literatur prakiraan cuaca, ini disebut sebagai statistik keluaran model (HR Glahn & Lowry, 1972 ; B. Glahn et al., 2009 ). Lovegrove dan Siegert ( 2023 ) menunjukkan dengan contoh prakiraan suhu global bahwa regresi linier sederhana yang sesuai menghasilkan interval prediksi untuk suhu yang memiliki probabilitas cakupan yang mendekati nominal; yaitu, (1-mathematical equation) interval prediksi yang diperoleh dari regresi linier sederhana mencakup nilai sebenarnya dengan probabilitas mendekati (1-mathematical equation) Di manamathematical equationadalah tingkat kesalahan liputan. Selain itu, pendekatan semacam itu telah digunakan untuk mengkalibrasi probabilitas yang dihasilkan dari model ML untuk kategori melalui regresi logistik, yang disebut sebagai penskalaan Platt (Platt et al., 1999 ).
Kami menerapkan pendekatan regresi linier ini sebagai berikut: untuk lokasi tertentu, kami meregresikan nilai perubahan permukaan laut yang disimulasikan ke prediksi emulator untuk semua data simulasi dalam set validasi menggunakan regresi linier sederhana. Ini juga mirip dengan metode split-conformal dari Lei et al. ( 2018 ) karena kami menggunakan set data yang dipisah dari data pelatihan asli untuk menyesuaikan model regresi linier, untuk menghindari overfitting dengan melatih model emulator dan model linier sederhana pada data yang sama. Namun, kami dapat meningkatkan cakupan bersyarat dengan menyesuaikan regresi linier yang berbeda untuk setiap lokasi. Selain itu, kovariat tambahan dapat dimasukkan ke dalam regresi linier untuk meningkatkan kalibrasi bersyarat. Selain itu, bias per lokasi diperhitungkan oleh istilah intersep dari model regresi linier sederhana.
Kami menggunakan interval prediksi standar dari model regresi linier sederhana yang disesuaikan:

Selama model linear merupakan kecocokan yang tepat antara pengamatan (yaitu, simulasi perubahan permukaan laut) dan prediksi emulator, interval prediksi harus mencakup probabilitas nominal. Pada Bagian 6 berikut, kami menunjukkan tingkat cakupan empiris pada serangkaian uji coba simulasi. Meskipun kami tidak mengeksplorasi distribusi residual alternatif atau korelasi spasial dalam residual, kami yakin item-item ini layak dieksplorasi dalam karya-karya mendatang. Meskipun demikian, metode split-conformal UQ yang dijelaskan berikutnya dengan mudah memungkinkan penyimpangan dari normalitas.
5.2 Inferensi Konformal Terpisah
Teknik modern yang lazim untuk mengukur ketidakpastian prediktif dari model ML adalah inferensi split-conformal (Lei et al., 2018 ). Inti dari pendekatan ini adalah menyesuaikan model ML pada set data pelatihan seperti biasa, tetapi menggunakan set data lain (misalnya, validasi) yang tidak digunakan untuk pelatihan guna membangun distribusi residual empiris. Kemudian, saat membuat prediksi untuk data uji yang tidak terlihat, seseorang menggunakan interval prediksi.mathematical equation, Di manamathematical equationadalah model ML yang pas,mathematical equationadalah residual yang dipilih dari distribusi residual empiris yang mengarah pada probabilitas cakupan tertentu (yaitu,mathematical equation), Danmathematical equationadalah contoh pengujian. Kami secara khusus menerapkan Algoritma 2 dari Lei et al. ( 2018 ) dalam menghitung interval prediksi pada hasil emulator berikut. Kami mencatat bahwa meskipun metode ini telah dikembangkan terutama dalam konteks model ML, metode ini dapat diterapkan pada fungsi apa pun yang disesuaikan termasuk pendekatan kernel sensitivitas berbasis fisika.
Metode UQ ini memiliki beberapa kelebihan dan kekurangan, yang dirangkum di sini. Kelebihannya antara lain tidak perlu melatih ulang model ML seperti dalam pendekatan resampling (yaitu, efisiensi komputasi), tidak ada asumsi distribusional pada residual, dan jaminan matematis dari probabilitas cakupan yang memenuhi tingkat nominal; dengan tingkat cakupan nominal, yang kami maksud adalah nilai yang dinyatakan darimathematical equation, misalnya, 95% untuk interval prediksi 95%. Namun, jaminan ini adalah rata-rata atas masukan, yang berarti bahwa beberapa kasus masukan dapat memiliki cakupan kurang dari tingkat nominal selama rata-rata memenuhi tingkat nominal. Terkait dengan itu, panjang interval tidak berubah untuk berbagaimathematical equationnilai, yaitu, wilayah ruang input (Dengan panjang interval prediksi, kami maksudkan batas atas interval dikurangi batas bawah interval). Namun, kami memperhitungkan variabilitas dalam residual di berbagai wilayah dalam aplikasi ini dengan menggunakan distribusi residual yang berbeda untuk setiap lokasi, sama seperti kami mempertimbangkan berbagai model regresi linier untuk setiap lokasi yang dibahas sebelumnya. Oleh karena itu, panjang interval prediktif berubah untuk lokasi yang berbeda dalam aplikasi kami. Kami mencatat bahwa meskipun metode ini dengan mudah memungkinkan penyimpangan dari kenormalan residual, metode ini tidak secara eksplisit memperhitungkan bias dalam prediksi, seperti yang dilakukan dengan istilah intersep regresi linier yang dijelaskan sebelumnya.
5.3 Pengambilan Sampel Variabel Laten dan Dropout Monte Carlo
Dua pendekatan UQ sebelumnya, inferensi split-conformal dan pasca-pemrosesan regresi linier, cukup generik dan dapat diterapkan ke semua metode emulasi (yaitu, pembelajaran mesin dan kernel sensitivitas berbasis fisika) yang diperiksa dalam studi ini. Namun, kami mencatat bahwa model ML CVAE yang dijelaskan dalam Bagian 3.2 adalah model ML generatif dan mengimplementasikan dropout Monte Carlo (MC) (Gal & Ghahramani, 2016 ), dan karenanya menambahkan metode lain yang mungkin untuk UQ. Dropout MC diimplementasikan dalam PyTorch dan pada dasarnya secara acak menolkan koneksi antara neuron di setiap lapisan dengan beberapa probabilitas yang telah ditentukan sebelumnya (kami menggunakan 0,3). Pengambilan sampel variabel laten normal standar dan melewatkannya melalui dekoder CVAE juga menambahkan sumber variabilitas lain dalam prediksi. Namun, ketika kami menerapkan metode UQ ini, kami menemukan bahwa cakupan interval prediktif yang secara nominal cakupannya 99+% (yaitu, sampel minimum dan maksimum) hanya mencakup keluaran sebenarnya 16% atau kurang dari waktu karena interval prediktif yang dihasilkan terlalu sempit. Kami mencatat bahwa jika MC dropout digunakan tanpa pengambilan sampel variabel laten, variabilitas dalam prediksi akan menjadi lebih kecil. Statistik ringkasan untuk tingkat cakupan empiris dan panjang interval rata-rata untuk interval nominal 99+% di 27 lokasi ditunjukkan dalam Tabel 1 dan 2 .
| menit | Kuartil ke-1 | Rata-rata | Berarti | Kuartil ke-3 | Maksimal |
|---|---|---|---|---|---|
| 0,017 tahun | 0,092 | 0.118 | 0.112 | 0.130 | 0,168 |
Catatan . Interval prediksi di sini berasal dari sampel prediktif minimum dan maksimum dan harus mendekati 0,99 atau lebih besar jika distribusi prediktif putus MC memiliki ketidakpastian yang terkalibrasi dengan baik, karena 500 sampel dihasilkan dengan putus MC.
| menit | Kuartil ke-1 | Rata-rata | Berarti | Kuartil ke-3 | Maksimal |
|---|---|---|---|---|---|
| 0,077 tahun | 0,084 tahun | 0,087 tahun | 0,086 tahun | 0,089 | 0,095 |
Catatan . Meskipun panjang ini sangat kecil, karena tingkat cakupan yang kecil, dapat disimpulkan bahwa distribusi prediktif putus MC sangat bias, yang menyiratkan UQ yang buruk.
Karena cakupan ini jauh lebih rendah dari tingkat nominal sementara distribusi prediktif dari putus sekolah MC sangat sempit, ini berarti distribusi prediktif dari pendekatan putus sekolah MC sangat bias dan kualitas UQ-nya buruk. Kami mengabaikan pendekatan ini untuk UQ dalam perbandingan berikut.
6 Hasil Emulator
Hasil utama kami terdiri dari perbandingan akurasi, tingkat cakupan interval prediksi empiris, dan panjang interval prediksi (didefinisikan sebagai batas atas dikurangi batas bawah interval prediksi) yang dihitung pada set uji hold-out. Kami menghitung koefisien korelasi determinasi Pearson,mathematical equation, selain root mean squared error (RMSE) antara prediksi emulator dan nilai perubahan permukaan laut simulasi aktual sebagai ukuran akurasi, meskipun ilustrasi pada Gambar 8 memberikan informasi lebih lanjut tentang akurasi. Boxplot pada Gambar 3 dan 4 menggambarkan rentang nilai untuk setiap emulator yang dibandingkan (yaitu, NN, CVAE, dan metode kernel sensitivitas) di 27 lokasi global yang berbeda dari studi ini. Dari Gambar 3 dan 4 , jelas bahwa kernel sensitivitas paling akurat, diikuti oleh CVAE, dan terakhir NN. Namun, CVAE mendekati kernel sensitivitas, dan untuk enam lokasi mencapai nilai yang lebih besarmathematical equationnilai. Kami mencatat bahwa kami juga mempertimbangkan variasi di mana inputnya bukan vektor yang diratakan tetapi berdasarkan sektor di Antartika (lihat Lampiran A ), meskipun akurasi dalam kasus itu jauh lebih buruk daripada hasil di sini, jadi kami tidak melanjutkannya lebih jauh.
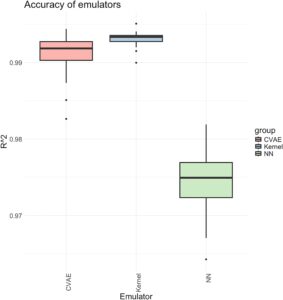
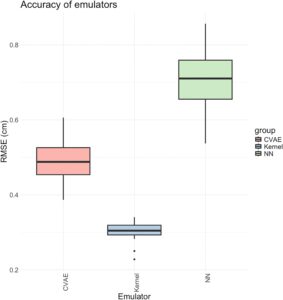
Kami juga melakukan uji peringkat bertanda Wilcoxon berpasangan untuk membandingkan akurasi secara statistik, yang diukur melaluimathematical equationdan RMSE, antara kernel dan CVAE serta kernel dan emulator NN. Uji peringkat bertanda Wilcoxon bersifat nonparametrik dan tidak mengasumsikan kenormalan. Kami memasangkan keduanyamathematical equationdan RMSE untuk masing-masing dari 27 lokasi ketika melakukan uji statistik ini. Nilai p dari semua pengujian sangat kecil, dengan yang terbesar adalahmathematical equation, mendukung alternatif bahwa emulator kernel lebih akurat (dalam hal RMSE yang lebih kecil dan lebih besarmathematical equation) daripada emulator NN atau CVAE.
Kami membandingkan tingkat cakupan empiris dan panjang interval prediksi sebagai sarana untuk menilai kualitas UQ untuk ketiga metode emulator dan untuk metode UQ split-conformal dan regresi linier. Kami menunjukkannya untuk nilai kesalahan cakupan nominalmathematical equation, dan 0,15 pada Gambar 5 dan 6. Temuan kami menunjukkan bahwa cakupan terbaik dicapai dengan metode split-conformal, meskipun panjang interval, terutama untukmathematical equation, mungkin terlalu besar untuk memiliki nilai praktis dalam aplikasi. Panjang interval prediktif untuk metode regresi linier jauh lebih berguna (dalam hal panjang) untuk nilai yang lebih kecilmathematical equationtapi interval ini menyamar terutama untukmathematical equation. Selain rasio cakupan empiris dan panjang interval prediksi, kami juga menghitung skor interval proper rata-rata (Gneiting & Raftery, 2007 ) per lokasi dan menampilkannya pada Gambar 7 ; temuan di sini serupa dengan analisis cakupan dan panjang, dalam hal skor split-conformal secara umum lebih rendah (yaitu, lebih baik), tetapi dalam 99% kasus split-conformal dan pendekatan model linier hampir terikat untuk metode kernel dan CVAE, dan sedikit lebih sedikit untuk metode NN yang menggunakan pendekatan model linier. Seperti yang diulas lebih lanjut dalam Gneiting dan Raftery ( 2007 ), aturan penilaian interval proper menggabungkan cakupan empiris dan panjang interval menjadi satu metrik, yang menghukum panjang interval prediksi serta miscoverage empiris relatif terhadap rasio nominal. Misalnya, jika nilai sebenarnya yang diprediksi adalah jarak tetap dari batas bawah interval prediksi, ini akan lebih dihukum untuk rasio cakupan nominal yang lebih tinggi.



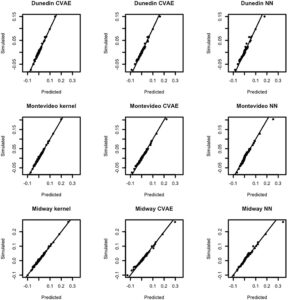
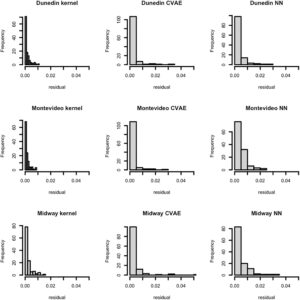
Gambar 8 menunjukkan ilustrasi yang menggambarkan hasil regresi linier yang digunakan untuk UQ untuk tiga lokasi yang mewakili variasi luas perubahan RSL di antara 27 kota: Midway, Montevideo, dan Dunedin. Ketiga lokasi yang dipilih dipilih karena mewakili variasi terluas dalam RSL di antara kota-kota yang dijadikan sampel (Gambar 1 ). Perubahan permukaan laut yang disimulasikan (yaitu, target prediksi) berada dimathematical equationPrediksi sumbu dan emulator ada dimathematical equation-axis. Setiap kolom mewakili tiga metode emulator dalam studi ini: NN, CVAE, dan metode kernel. Selain itu, kami memetakan histogram residual yang diturunkan untuk digunakan dalam inferensi split-conformal pada Gambar 9. Residu ini menunjukkan bahwa skala kesalahan adalah yang terkecil untuk metode kernel, yang selanjutnya menguatkan klaim bahwa metode ini adalah yang paling akurat dari metode emulasi yang dibandingkan.
Kami juga menilai waktu proses untuk menghasilkan prediksi dengan masing-masing model ML dengan melakukan satu tugas prediksi sebanyak 1.000 kali. Semua 1.000 prediksi NN diselesaikan dalam waktu kurang dari 0,25 detik dan semua kecuali satu dari proses CVAE diselesaikan dalam waktu kurang dari 0,375 detik. Kami menganggap bahwa satu prediksi selesai ketika model memberikan nilai prediksi untuk semua 27 lokasi. Untuk model CVAE, waktu proses diukur berdasarkan satu sampel yang diambil dari distribusi laten yang diasumsikan. Kami juga mengamati bahwa langkah kalibrasi tambahan tidak berkontribusi pada peningkatan waktu proses yang signifikan (mathematical equation0,0006 d). Pelatihan setiap emulator ML memakan waktu sekitar beberapa jam di atas overhead 21 jam (17 menit per satu kali jalan, dikali 71 kali jalan) untuk menjalankan kalkulasi sidik jari permukaan laut secara serial. Sebaliknya, waktu jalan metode kernel disebabkan oleh perkalian matriks-vektor dan hanya memerlukan satu penyelesaian maju untuk menghasilkan kernel sensitivitas dan dengan demikian overhead yang jauh lebih sedikit daripada NN dan CVAE untuk pelatihan. Metode kernel membutuhkan waktu rata-rata dan median 5,2 d untuk menghasilkan nilai perubahan permukaan laut yang diemulasikan untuk semua 27 lokasi yang diminati untuk semua 17 tingkat waktu; dengan demikian membutuhkan waktu 0,3 d untuk membuat prediksi di semua 27 lokasi, yang mendekati waktu jalan CVAE dan NN. Selain itu, metode kernel membutuhkan waktu 33 d untuk menghasilkan kernel untuk 27 kota. Mengingat penyelesaian penuh memerlukan waktu sekitar 60 detik per tingkat waktu, semua metode emulasi mampu meningkatkan kecepatan hingga lebih dari 100 kali lipat dibandingkan menjalankan simulasi penuh untuk menghasilkan sidik jari permukaan laut; namun, kami tekankan bahwa overhead pembangkitan kernel untuk metode kernel jauh lebih kecil daripada overhead pelatihan untuk metode ML.
Pada Tabel 3 , kami merangkum biaya komputasi untuk emulator untuk tiga langkah: (a) menghasilkan sidik jari permukaan laut melalui penyelesai permukaan laut numerik, (b) melatih emulator pada data pelatihan, dan (c) mengevaluasi emulator untuk membuat prediksi untuk 27 lokasi yang diminati.
| Emulator | Pembuatan data (min) | Pemasangan emulator (min) | Waktunya untuk prediksi |
|---|---|---|---|
| Kernel sensitivitas | 1 | Bahasa Indonesia | 0.31 |
| Tidak ada | 969 | 121 | 0,25 |
| CVAE | 969 | 286 | 0,375 tahun |
Catatan . Perhatikan bahwa untuk metode kernel, kernel untuk setiap lokasi dibuat setelah menjalankan sea-level solver sehingga tidak diperlukan pelatihan tambahan (berbeda dengan metode ML). Model ML dilatih menggunakan partisi unit pemrosesan grafis (GPU) bersama yang tersedia dari kluster Darwin (Garrett, 2018 ) di Laboratorium Nasional Los Alamos.
7 Aplikasi Emulator untuk Monte Carlo Ensemble
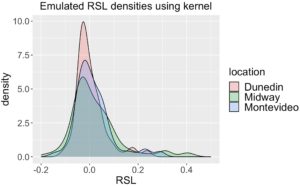
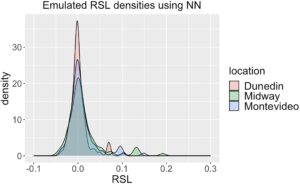
Kami menunjukkan potensi penggunaan emulator perubahan permukaan laut untuk menghasilkan distribusi keluaran simulasi perubahan permukaan laut untuk lokasi di seluruh dunia, guna menunjukkan bagaimana emulator tersebut dapat digunakan untuk menghasilkan distribusi RSL dari simulasi lapisan es Antartika di masa mendatang. Pendekatan Monte Carlo yang paling mudah untuk melakukannya adalah dengan mengambil sampel banyak parameter dari distribusinya masing-masing, menjalankan simulator lapisan es di bawah parameter yang diambil sampelnya, dan kemudian menjalankan status lapisan es yang dihasilkan melalui emulator perubahan permukaan laut guna menghasilkan distribusi nilai perubahan permukaan laut. Untuk tujuan kami, menjalankan simulator lapisan es secara iteratif sangat mahal dan karenanya kami membangun ensembel Monte Carlo dari status lapisan es menggunakan ensembel simulasi Antartika ISMIP6.
Sasaran kami dalam demonstrasi ini adalah menggunakan kernel dan emulator NN untuk menghasilkan distribusi nilai perubahan permukaan laut untuk 27 lokasi pengukur pasang surut jangka panjang. Untuk contoh ini, kami fokus pada tahun 2100 dan skenario emisi tinggi, dan menyaring 48 contoh dari data pelatihan ISMIP6 yang sesuai dengan kriteria ini. Kami melakukan analisis komponen utama pada 48 contoh ini, mempertahankan 32 teratas yang menjelaskan 99% variasi dalam simulasi emisi tinggi tahun 2100. Kami kemudian melakukan bootstrap bobot komponen utama 100 kali untuk secara acak menghasilkan ansambel Monte Carlo dari negara-negara lapisan es Antartika yang mewakili tahun 2100 dan emisi tinggi. Teknik reduksi dimensi alternatif dapat dieksplorasi, meskipun pendekatan komponen utama digunakan sebagai metode praktis untuk menghasilkan ansambel Monte Carlo. 100 negara lapisan es yang dihasilkan secara acak ini kemudian dimasukkan ke dalam kernel dan emulator jaringan saraf. Kami mengilustrasikan kepadatan perubahan permukaan laut yang ditiru menggunakan simulasi Monte Carlo pada Gambar 10 dan 11. Kami menekankan bahwa distribusi ini hanya dimaksudkan sebagai demonstrasi penerapan emulator.