Abstrak
Jaringan saraf graf (GNN) telah banyak digunakan dalam ilmu material karena kemampuannya untuk memproses data terstruktur graf yang kompleks dengan menangkap hubungan antara atom, molekul, atau struktur kristal dalam material. Namun, karena kurangnya interpretabilitas, GNN bertindak sebagai model “kotak hitam” dalam banyak kasus. Dalam karya ini, dengan memperkenalkan mekanisme perhatian ke dalam GNN, model jaringan saraf perhatian graf (GANN) untuk material 2D diusulkan, yang tidak hanya mencapai kinerja prediksi yang akurat tetapi juga menunjukkan interpretabilitas melalui analisis mekanisme perhatian. Mengambil heterostruktur Janus III–VI van der Waals sebagai kasus representatif, MAE untuk memprediksi energi pembentukan, konstanta kisi, celah pita PBE, dan celah pita HSE06 masing-masing adalah 0,009 eV, 0,003 Å, 0,087, dan 0,123 eV. Hebatnya, model GANN menunjukkan kemampuan generalisasi yang luar biasa yang dapat mencapai prediksi akurat menggunakan struktur masukan yang ditebak tanpa relaksasi struktural sepenuhnya untuk mencapai keadaan dasar bagi heterostruktur Janus III–VI vdW. Lebih jauh, mekanisme perhatian integrasi memungkinkan analisis kualitatif atas kontribusi atom-atom tetangga terdekat, yang memberikan model GNN dengan interpretabilitas yang ditingkatkan. Temuan kami menawarkan perspektif baru untuk desain material 2D yang digerakkan oleh AI dengan membangun keseimbangan optimal antara akurasi prediktif dan interpretabilitas model dalam pendekatan GNN.
1 Pendahuluan
Kemajuan pesat kecerdasan buatan telah mendorong penelitian ilmiah secara signifikan, dengan pembelajaran mesin (ML) muncul sebagai alat yang ampuh [ 1 – 3 – 4 ]. Dalam ilmu material, ML telah diterapkan secara luas pada penelitian dan desain keramik [ 5 ], material kristal tunggal [ 6 ], material feroelektrik [ 7 ], perovskit [ 8 ], dkk. Di antara berbagai model ML, jaringan saraf grafik (GNN) [ 9 , 10 ], sebagai arsitektur pembelajaran mendalam yang inovatif, telah mendapatkan perhatian global atas kemampuannya untuk memodelkan konfigurasi atom dan molekul sebagai grafik, secara efektif menangkap hubungan linier dan nonlinier yang kompleks dalam material [ 11 , 12 – 13 ]. Kinerja yang luar biasa berkontribusi pada keberhasilan penerapan GNN di berbagai bidang seperti katalisis [ 14 ], baterai berbasis litium [ 15 ], sel surya [ 16 ], dan seterusnya [ 17 ]. Meskipun demikian, meskipun model GNN menawarkan banyak keuntungan, keterbatasan interpretabilitasnya menimbulkan tantangan besar untuk aplikasi yang lebih luas dalam ilmu material [ 18 , 19 ].
Teknik ML yang dapat diinterpretasikan adalah solusi yang memungkinkan untuk memecahkan masalah interpretabilitas untuk model kecerdasan buatan dalam ilmu material dengan kemungkinan untuk mengungkap hubungan fisik fundamental antara fitur input dan properti target, dengan demikian menjembatani kesenjangan antara model berbasis data dan wawasan fisik spesifik domain [ 20 – 23 – 24 ]. Misalnya, operator penyaringan dan penghalusan independensi pasti (SISSO) yang dikembangkan [ 25 ] dapat membangun ruang fitur kompleks melalui kombinasi operasi aljabar dan fungsional untuk mendapatkan rumus matematika atau deskriptor yang terkait secara linier dengan variabel target, yang telah digunakan dalam menjelaskan stabilitas dan kinerja sel surya perovskit [ 22 , 26 ], polarisasi bahan kalium niobat [ 27 , 28 ], dan katalis logam [ 23 ]. Namun, pendekatan ML yang dapat diinterpretasikan konvensional masih menunjukkan kinerja prediktif yang kurang optimal, terutama saat menangani ruang deskriptor berdimensi tinggi atau memodelkan hubungan struktur-properti nonlinier. Menarik untuk dicatat bahwa mekanisme perhatian menawarkan solusi potensial dengan menimbang distribusi fitur input secara dinamis, secara selektif meningkatkan informasi penting sambil menekan elemen yang tidak relevan [ 29 , 30 – 31 ]. Mengintegrasikan mekanisme perhatian ke dalam GNN memungkinkan penugasan bobot adaptif selama penyampaian pesan, sehingga meningkatkan interpretabilitas model sambil mempertahankan akurasi prediktif [ 32 , 33 ].
Bahan Janus 2D, sebagai kelas bahan 2D yang sedang berkembang, telah menarik perhatian signifikan karena sifat fisik dan kimianya yang unik yang timbul dari konfigurasi atom asimetris pada permukaan yang berlawanan [ 34 , 35 ]. Lapisan tunggal Janus III–VI, dengan rumus kimia MM’XX’ (M, M’ = Ga dan In dan X, X’ = S, Se, dan Te), telah menarik perhatian yang luas karena struktur elektronik dan sifat optiknya yang dapat disetel [ 36 ]. Di sisi lain, dengan menumpuk lapisan tunggal Janus III–VI yang berbeda, heterostruktur van der Waals (vdW) Janus III–VI dapat dibangun, menawarkan kinerja fisik dan kimia yang menjanjikan untuk aplikasi potensial perangkat elektronik dan optoelektronik berkinerja tinggi generasi berikutnya [ 37 , 38 ]. Namun, karena keragaman komposisi kimia dan struktur lapisan tunggal Janus III–VI, jumlah heterostruktur vdW Janus III–VI yang mungkin sangat banyak. Dalam pekerjaan kami sebelumnya [ 36 ], database heterostruktur Janus III–VI vdW komputasional throughput tinggi telah dibuat menggunakan platform otomatis ALKEMIE [ 39 ]. Oleh karena itu, model GNN yang akurat diusulkan menurut database komputasional throughput tinggi; meskipun demikian, model GNN kurang interpretatif [ 36 ]. Di sisi lain, kami telah menggunakan kerangka kerja SISSO untuk mendapatkan hubungan eksplisit antara fitur komposisi/struktural dan celah pita untuk heterostruktur Janus III–VI vdW; namun, akurasi model SISSO tidak dapat dibandingkan dengan model GNN [ 40 ]. Dengan demikian, mengembangkan kerangka kerja yang secara bersamaan mencapai presisi tinggi dan interpretatif model ML untuk heterostruktur Janus III–VI vdW tetap sangat penting.
Dalam karya ini, kami mengembangkan kerangka kerja graph attention neural network (GANN) yang meningkatkan presisi dan interpretabilitas dalam prediksi properti untuk heterostruktur Janus III–VI vdW. Kerangka kerja ini secara akurat memprediksi konstanta kisi, energi pembentukan, dan celah pita (baik untuk fungsional perdew-burke-ernzerhof (PBE) maupun fungsional hibrida heyd-scuseria-ernzerhof (HSE06)). Hebatnya, model tersebut tetap dapat memastikan akurasi tinggi bahkan saat menggunakan struktur tebakan tanpa relaksasi struktural penuh sebagai set pengujian generalisasi, yang menunjukkan properti yang dapat digeneralisasi dari kerangka kerja kami. Selain itu, analisis koefisien perhatian mengungkapkan pengaruh relatif dari atom yang berbeda pada prediksi model, yang menawarkan panduan teoritis untuk prediksi dan penyaringan properti dalam heterostruktur Janus III–VI vdW.
2 Metode
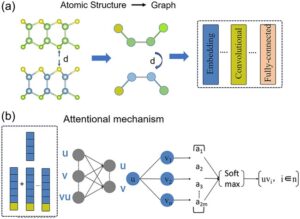
GNN adalah jaringan saraf yang secara inheren memproses data berstruktur grafik melalui kerangka kerja penyampaian pesan, yang didasarkan pada teori grafik spektral. Dibandingkan dengan jaringan saraf tradisional, perbedaan yang paling jelas adalah bahwa struktur grafis yang hanya terdiri dari simpul dan tepi digunakan sebagai input dalam GNN [ 41 , 42 ]. Struktur grafis ini terdiri dari simpul dan tepi, yang sesuai dengan atom dan ikatan dalam heterostruktur Janus III–VI vdW.
![]()
di mana V (vektor simpul) merepresentasikan vektor fitur elemen dari setiap atom dan E (vektor tepi) merepresentasikan ikatan antara setiap dua atom, seperti yang ditunjukkan pada Gambar 1 a. Kami memperkenalkan kerangka kerja mekanisme perhatian berdasarkan model GNN standar untuk mendapatkan model GANN baru, seperti yang ditunjukkan pada Gambar 1 b. Di sini, tensor baru dihasilkan melalui lapisan yang terhubung penuh yang diterapkan pada setiap simpul ( atom u ), yang mengintegrasikan informasi dari atom tetangga ( v ) dan tepi yang sesuai ( vu ) berdasarkan parameter yang telah ditentukan sebelumnya, seperti jumlah maksimum atom tetangga. Selanjutnya, vektor baru yang mewakili atom u yang diberikan dan semua atom tetangganya vn digabungkan. Kemudian, untuk atom u yang diberikan , skor perhatian untuk semua atom tetangga vn dihitung menggunakan fungsi Softmax dan disempurnakan secara iteratif melalui algoritma backpropagation. Deskripsi terperinci disediakan dalam Persamaan ( 2 )–( 5 ) [ 43 , 44–45 ] .
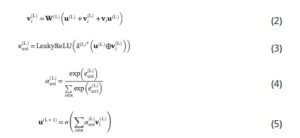
Pada Persamaan ( 2 ),mathematical equationadalah matriks bobot yang dapat dipelajari dari lapisan L danmathematical equationadalah vektor fitur dari simpul i di lapisan L. Setelah transformasi linier, skor perhatian yang tidak dinormalisasi berpasanganmathematical equationakan dihitung antara setiap pasangan tetanggamathematical equationberpusat pada titik puncak i pada Persamaan ( 3 ). ⊕ menunjukkan penggabungan;mathematical equationadalah vektor bobot yang dapat dipelajari yang digunakan untuk melakukan perkalian titik dengan vektor yang dirangkai. LeakyReLU adalah fungsi aktivasi. Persamaan ( 4 ) adalah fungsi Softmax untuk menormalkan skor perhatian [ 45 ]. Pada akhirnya, informasi dari semua simpul tetangga dari simpul u digabungkan, dan vektor fitur dari simpul u digunakan dalam lapisan L + 1. Jelas bahwa setelah proses yang disebutkan di atas, setiap simpul dapat secara efektif menggabungkan informasi dari semua atom tetangganya. Di sini, mekanisme perhatian memperoleh bobot melalui lapisan yang terhubung penuh berdasarkan fitur grafik global atau lokal (misalnya, pengumpulan rata-rata fitur simpul), sebuah proses yang secara implisit mengintegrasikan interaksi ‘kunci kueri’. Bobot ini kemudian dikalikan dengan fitur (bertindak sebagai ‘nilai’) untuk menekankan informasi penting, menyoroti atom dengan bobot tinggi yang mendominasi sifat fisik tertentu.
Selanjutnya, dengan mengambil heterostruktur Janus III–VI vdW sebagai kasus representatif, kami menggunakan kerangka kerja GANN untuk memprediksi properti yang relevan. Basis data dibagi menjadi set pelatihan, set validasi, dan set pengujian dalam rasio 8 : 1:1, dengan 80% data digunakan untuk melatih model, 10% data digunakan untuk memvalidasi model, dan 10% data digunakan untuk menguji model. Perlu dicatat bahwa struktur heterostruktur Janus III–VI vdW dalam basis data awal direlaksasi penuh untuk mencapai keadaan dasar. Ambang konvergensi energi dan ambang konvergensi gaya interatomik ditetapkan masing-masing pada 10 −6 eV dan 0,05 eV/Å. Lebih jauh, untuk memvalidasi kemampuan generalisasi kerangka kerja GANN, kami selanjutnya menggunakan struktur masukan tanpa relaksasi struktural sebagai masukan dari set pengujian generalisasi tambahan untuk memprediksi properti target. Hiperparameter yang diadopsi untuk pekerjaan ini tercantum dalam Tabel S1. Selanjutnya, semua kode dan skrip pelatihan yang terkait dengan studi ini, termasuk jalur komprehensif untuk praproses data, pelatihan model, dan analisis hasil, tersedia untuk umum di GitHub ( https://github.com/syd-c/GANN.git ) di bawah lisensi sumber terbuka.
3 Hasil dan Pembahasan
3.1 Kumpulan Data
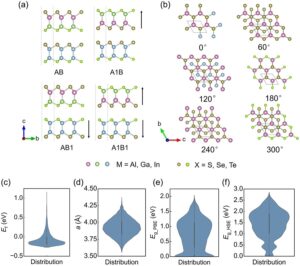
Basis data untuk heterostruktur Janus III–VI vdW [ 36 , 38 ] dibangun menggunakan platform ALKEMIE [ 34 ] dengan throughput tinggi dari 45 lapisan tunggal Janus III–VI, yang dapat dibagi menjadi empat kategori: MX, MM’X2 , M2XX ‘ , dan MM’XX’ (M, M’ = Al, Ga dan In, X, X’ = S, Se, dan Te), di mana MM’ dan XX’ menunjukkan elemen M dan X yang berbeda dalam lapisan tunggal. Dengan mempertimbangkan konfigurasi susunan yang berbeda, heterostruktur dapat diklasifikasikan menjadi empat jenis: susunan langsung tanpa pembalikan (AB), pembalikan lapisan atas asimetris cermin ( A1B ), pembalikan lapisan bawah (AB1 ) , dan pembalikan lapisan ganda secara bersamaan (A1B1 ) , seperti yang diilustrasikan dalam Gambar 2a . Hasilnya, 3.321 heterostruktur Janus III–VI dibangun. Selanjutnya, enam kemungkinan konfigurasi penumpukan dengan memutar 0°, 60°, 120°, 180°, 240°, dan 300° dari lapisan atas dari 3321 heterostruktur Janus III–VI di atas dipertimbangkan lebih lanjut, seperti yang diilustrasikan dalam Gambar 2 b. Akhirnya, sejumlah total 19926 heterostruktur Janus III–VI vdW dihasilkan untuk perhitungan teori fungsional densitas throughput tinggi. Properti berikut untuk heterostruktur Janus III–VI vdW dipertimbangkan untuk pelatihan model GANN: energi pembentukan ( E f ), konstanta kisi ( a ), celah pita PBE ( E g_PBE ), dan celah pita HSE06 ( E g_HSE ), termasuk 13284, 19926, 13284, dan 6321 titik data, masing-masing. Distribusi E f , a , E g_PBE , dan E g_HSE masing-masing direpresentasikan pada Gambar 2c–f . Rincian lebih lanjut mengenai database heterostruktur Janus III–VI vdW dapat dilihat pada karya kami sebelumnya [ 36 ].
3.2 Kinerja Model GANN
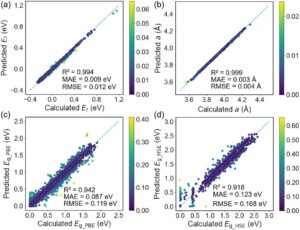
Performa model GANN dari set pengujian untuk heterostruktur Janus III–VI vdW ditunjukkan pada Gambar 3. Dalam kasus ideal, semua titik data berada pada garis diagonal, yang menunjukkan bahwa nilai prediksi sama dengan nilai sebenarnya. Namun, dalam praktiknya, mungkin ada beberapa deviasi antara nilai prediksi dan nilai sebenarnya, dan deviasi z didefinisikan sebagai
![]()
di mana y test menyajikan nilai sebenarnya dan y pre mewakili nilai prediksi. Pada Gambar 3 , z dipetakan oleh batang warna. Di sini,mathematical equationberfungsi sebagai faktor skala untuk mengompresi rentang nilai kesalahan, menghasilkan distribusi batang warna yang lebih seragam yang secara signifikan meningkatkan keterbacaan diagram sebar. Diperlihatkan pada Gambar 3a,b bahwa model GANN menunjukkan akurasi prediksi yang sangat baik untuk energi pembentukan dan konstanta kisi heterostruktur Janus III–VI vdW, di mana nilai R 2 masing-masing adalah 0,994 dan 0,999, nilai MAE masing-masing adalah 0,009 eV dan 0,003 Å, dan nilai RMSE masing-masing adalah 0,012 eV dan 0,004 Å. Perlu dicatat bahwa kinerja prediksi untuk celah pita PBE juga berjalan sangat baik dengan nilai R 2 , MAE, dan RMSE masing-masing sebesar 0,942, 0,087, dan 0,119 eV, seperti yang ditunjukkan pada Gambar 3c . Di sisi lain, hasil prediksi celah pita HSE06 menunjukkan beberapa distribusi diskret daripada hasil prediksi PBE, seperti yang ditunjukkan pada Gambar 3d . MAE yang sedikit lebih tinggi untuk prediksi celah pita HSE06 dibandingkan dengan PBE terutama berasal dari faktor-faktor berikut. (1) Keterbatasan volume data: Dataset celah pita HSE06 (6321 entri) secara signifikan lebih kecil daripada dataset PBE, yang menyebabkan berkurangnya kemampuan pemasangan model untuk nilai celah pita HSE06. (2) Analisis kesalahan relatif: Meskipun MAE absolut yang lebih tinggi untuk HSE06, nilai R 2 (0,918) tetap sebanding dengan PBE (0,942), yang menunjukkan bahwa model tersebut secara efektif menangkap tren keseluruhan dalam celah pita. Meskipun demikian, nilai R 2 , MAE, dan RMSE untuk prediksi celah pita HSE06 masing-masing adalah 0,918, 0,123, dan 0,168 eV. Oleh karena itu, kita dapat menyimpulkan bahwa model GANN secara akurat memprediksi nilai celah pita heterostruktur Janus III–VI vdW untuk fungsional PBE dan HSE06.
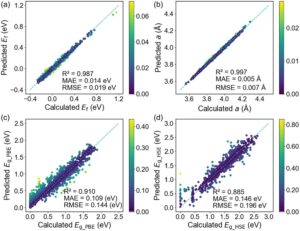
Untuk menguji lebih lanjut kemampuan generalisasi model GANN, kami menyertakan struktur tebakan tambahan untuk heterostruktur Janus III–VI vdW tanpa relaksasi struktural penuh sebagai set pengujian generalisasi. Dengan menggunakan struktur tebakan sebagai fitur masukan, kinerja prediksi model GANN untuk heterostruktur Janus III–VI vdW ditunjukkan pada Gambar 4. Menariknya, kinerja prediksi keseluruhan model GANN secara mengejutkan bagus meskipun struktur masukan tidak direlaksasi untuk mencapai keadaan dasar. Seperti yang ditunjukkan pada Gambar 4 a,b, untuk prediksi energi pembentukan dan konstanta kisi heterostruktur Janus III–VI vdW, akurasi prediksi yang sangat baik dikonfirmasi oleh nilai R 2 masing-masing sebesar 0,987 dan 0,997, nilai MAE masing-masing sebesar 0,014 eV dan 0,005 Å, dan nilai RMSE masing-masing sebesar 0,019 eV dan 0,007 Å. Seperti yang ditunjukkan pada Gambar 4 c, kinerja prediksi yang luar biasa untuk celah pita PBE juga dicapai dengan nilai R 2 , MAE, dan RMSE masing-masing sebesar 0,910, 0,109, dan 0,144 eV. Pada saat yang sama, distribusi prediksi celah pita HSE06 pada Gambar 4 d mirip dengan yang menggunakan struktur yang sepenuhnya rileks, distribusi diskrit yang diamati untuk heterostruktur Janus III–VI vdW dengan nilai celah pita HSE06 yang dihitung kurang dari 0,5 eV. Bagaimanapun, untuk prediksi celah pita HSE06, kinerja model GANN sangat baik dengan nilai R 2 , MAE, dan RMSE masing-masing sebesar 0,885, 0,146, dan 0,196 eV. Hebatnya, hasil kami menunjukkan bahwa model GANN mempertahankan akurasi prediktif yang tinggi bahkan ketika diterapkan pada struktur yang ditebak tanpa relaksasi struktural penuh, seperti yang divalidasi dalam set pengujian generalisasi.
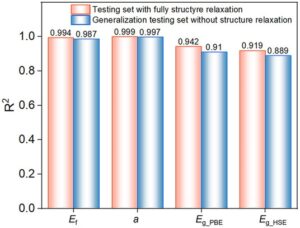
Sangat penting untuk dicatat bahwa hiperparameter awal dan partisi dataset identik. Oleh karena itu, kinerja prediksi model GANN dengan dan tanpa relaksasi struktural penuh dari set pengujian dan pengujian generalisasi sebanding. Perbedaan kinerja antara input dengan dan tanpa relaksasi struktural penuh direpresentasikan dalam Gambar 5. Dapat diamati bahwa perbedaannya dapat diabaikan untuk memprediksi energi pembentukan dan konstanta kisi. Selain itu, kinerja untuk memprediksi celah pita PBE dan celah pita HSE06 juga dekat. Karena relaksasi struktur material adalah salah satu langkah utama yang memakan waktu dalam perhitungan teori fungsi kerapatan, kinerja generalisasi model GANN yang luar biasa dapat lebih mempercepat prediksi tanpa mengorbankan akurasi, yang sangat menarik dan penting.
3.3 Analisis Mekanisme Perhatian
Properti umum yang diusulkan dari model GANN menunjukkan bahwa model tersebut telah menangkap hubungan fisik potensial antara fitur struktur masukan dan properti prediksi, karena komposisi kimia dan struktur grafik tetap tidak berubah sebelum dan setelah relaksasi struktur penuh. GNN telah berfungsi sebagai model “kotak hitam”, tetapi kerangka kerja dalam karya ini termasuk mekanisme perhatian dapat membantu kita dalam memahami hubungan intrinsik. Di sini, bobot perhatian yang dapat dipelajari diperkenalkan dalam mekanisme perhatian, yang membuat kerangka kerja GANN secara dinamis berfokus pada pentingnya berbagai simpul. Dengan mengambil prediksi celah pita PBE sebagai contoh, enam set heterostruktur disaring untuk menganalisis interaksi antara atom yang berbeda. Kriteria penyaringan adalah sebagai berikut. (1) Perbedaan antara nilai yang dihitung dan diprediksi harus kurang dari 0,06 eV untuk heterostruktur di setiap set. (2) Komposisi kimia heterostruktur di setiap set hanya berbeda satu atom, di mana atom ‘Self’ mewakili atom yang berbeda dalam dua heterostruktur yang serupa.
Koefisien perhatian dari 12 atom tetangga terdekat dengan atom Self di setiap set heterostruktur diilustrasikan dalam Gambar 6. Misalnya, dalam Gambar 6a , atom Self adalah atom Ga dan In untuk heterostruktur GaAlSe2 / SeInGaTe dan InAlSe2 / SeInGaTe vdW, masing-masing. Menarik untuk dicatat bahwa atom Self selalu menunjukkan skor perhatian minimal, yang mungkin bukan faktor kunci untuk mendominasi celah pita PBE dari heterostruktur Janus III–VI vdW. 12 atom yang berdekatan pada sumbu x disusun dari kiri ke kanan berdasarkan jaraknya dari atom Self. Angka-angka yang mengikuti elemen menunjukkan urutan elemen dalam berkas struktur yang ditransformasikan (0–3 mewakili empat elemen dari lapisan tunggal Janus III–VI atas, dan 4–7 mewakili lapisan tunggal Janus III–VI bawah).

Dengan mengamati kontribusi atom-atom tetangga terdekat terhadap atom Self dalam setiap set heterostruktur, semua 12 atom terletak dalam lapisan tunggal Janus III–VI yang sama. Hasil ini dapat dikaitkan dengan fakta bahwa model tersebut terutama mempelajari koefisien perhatian untuk atom-atom tetangga terdekat dalam lapisan tunggal yang sama. Seperti yang diilustrasikan dalam Gambar 6 a, skor perhatian yang jauh lebih tinggi diberikan kepada atom Al3, yang menunjukkan pengaruh yang lebih kritis dibandingkan dengan atom-atom penyusun lainnya. Oleh karena itu, atom Al3 memainkan peran dominan dalam modulasi celah pita PBE untuk heterostruktur GaAlSe 2 /SeInGaTe dan InAlSe 2 /SeInGaTe vdW. Seperti yang diverifikasi oleh struktur pita yang diproyeksikan dalam Gambar S1, atom Al3 terutama mengatur minimum pita konduksi dari heterostruktur GaAlSe 2 /SeInGaTe dan InAlSe 2 /SeInGaTe, yang menunjukkan peran kritisnya dalam memodulasi nilai celah pita. Tren yang konsisten telah diamati dalam Gambar 6 b–d. Di sisi lain, koefisien perhatian dari 12 atom tetangga menunjukkan tren yang konsisten dengan jaraknya, seperti yang ditunjukkan pada Gambar 6 e,f. Secara khusus, pengaruh pada atom pusat berkurang dengan meningkatnya jarak [ 46 , 47 ]. Akibatnya, koefisien perhatian ini berfungsi sebagai fitur tambahan untuk mengungkap pengaruh dari kontribusi atom tetangga terdekat dan karenanya meningkatkan interpretabilitas model GANN.
4 Kesimpulan
Singkatnya, kami telah mengembangkan GNN yang mengintegrasikan mekanisme perhatian untuk mencapai prediksi properti yang akurat untuk heterostruktur Janus III–VI vdW. MAE untuk memprediksi energi pembentukan, konstanta kisi, celah pita PBE, dan celah pita HSE06 dari heterostruktur Janus III–VI vdW 2D masing-masing adalah 0,012 eV, 0,004 Å, 0,119, dan 0,168 eV, yang menyoroti kemampuan generalisasi model yang kuat. Hebatnya, model tersebut dapat secara akurat memprediksi properti heterostruktur Janus vdW 2D; bahkan fitur input adalah struktur tanpa relaksasi struktural, yang secara efektif mengatasi tantangan ganda dari struktur yang memakan waktu dengan relaksasi struktural penuh. Lebih jauh, kontribusi atom tetangga terdekat dapat dianalisis dengan memperkenalkan mekanisme perhatian dalam kerangka kerja. Pada akhirnya, kami mengembangkan kerangka kerja berkinerja tinggi yang dapat diinterpretasikan yang menjembatani wawasan skala atom dengan prediksi properti makroskopis, yang menawarkan kerangka kerja transformatif untuk mempercepat desain material 2D fungsional.
