Abstrak
Studi ini menyajikan pendekatan kontrol baru, yang disebut kontrol impedansi hibrida fraksional adaptif (AFH-IC), untuk aktuator elastis seri putar (RSEA) yang beroperasi di medan datar, seperti lantai padat (keras), karpet (sedang), dan rumput (lunak). Tujuan utamanya adalah untuk mengembangkan sistem kontrol torsi dan posisi bersensitivitas tinggi yang mampu menangani berbagai lintasan gerak, termasuk perubahan keras yang tiba-tiba. Tidak seperti metode kontrol impedansi tradisional, AFH-IC, yang disempurnakan dengan kontrol orde fraksional dan algoritma fuzzy adaptif, dirancang untuk menghilangkan kesalahan torsi dalam lingkungan kekakuan yang bervariasi terhadap waktu. Parameter fraksional AFH-IC dioptimalkan menggunakan pengoptimalan kumpulan partikel untuk setiap medan dengan batasan yang berbeda. RSEA yang dirancang khusus digunakan dalam simulasi dan eksperimen. Struktur kontrol yang diusulkan menunjukkan kinerja yang unggul dibandingkan dengan metode konvensional seperti kontrol impedansi hibrida fraksional dan kontrol impedansi hibrida. Hasilnya menegaskan bahwa AFH-IC secara signifikan meningkatkan akurasi dan ketahanan pelacakan gaya dalam aplikasi dunia nyata.
1 Pendahuluan
Mencapai posisi yang cepat dan akurat serta kendali lintasan gaya merupakan persyaratan mendasar dalam berbagai aplikasi robotik, termasuk robot berkaki, [ 1 ] sistem haptik, [ 2 ] robotika medis, manipulator lengan panjang, [ 3 ] robot rehabilitasi, [ 4 ] dan sistem robotik khusus. [ 5 ] Banyak dari sistem ini bergantung pada aktuator yang dipisahkan dari beban melalui antarmuka fleksibel, yang meningkatkan kepatuhan, efisiensi energi, dan keamanan sekaligus mengurangi tekanan mekanis. Di antara ini, aktuator elastis seri (SEA) sangat menguntungkan karena kemampuannya untuk mencapai kendali gerak yang hemat energi, responsif secara dinamis, dan patuh. [ 6 ]
Untuk aplikasi tertentu, aktuator elastis seri putar (RSEA) lebih disukai daripada SEA tradisional karena kemampuan adaptasi dan fleksibilitas rotasinya yang lebih baik. Namun, penerapan kontrol impedansi yang tepat di RSEA tetap menjadi tantangan, karena memerlukan penyeimbangan pelacakan torsi dan pengaturan posisi saat berinteraksi dengan lingkungan yang dinamis dan tidak pasti. [ 7 ] Strategi kontrol konvensional, seperti kontrol impedansi (IC) dan kontrol hibrid (HC), telah banyak digunakan untuk mengatur torsi sambungan pada aktuator robotik.
Dalam mekanisme gerakan anggota tubuh, kontrol impedansi terutama mengatur hubungan antara posisi dan torsi pada titik interaksi daripada mengendalikan torsi secara langsung. [ 8 ] Pendekatan ini sering kali bergantung pada kontrol berbasis posisi untuk menyesuaikan torsi. Sebaliknya, HC membagi kerangka kontrol impedansi menjadi dua subruang independen: kontrol torsi dan kontrol posisi. [ 9 ] Anderson dan Spong [ 10 ] memperkenalkan pengontrol impedansi hibrida (H-IC), yang menggabungkan kedua subruang ini untuk mencapai kinerja kontrol yang lebih baik. [ 11 ]
Baru-baru ini, pengendali orde fraksional (FOC) telah dieksplorasi sebagai cara yang efektif untuk meningkatkan karakteristik respons frekuensi dalam sistem robotik. Pengendali ini memungkinkan penyesuaian yang tepat menggunakan diferensiasi dan integrasi fraksional, yang memungkinkan penanganan perilaku dinamis yang kompleks dengan lebih baik. [ 12 ] Penelitian telah menunjukkan bahwa pengendali impedansi hibrida fraksional (FH-IC), yang mengintegrasikan FOC ke dalam kerangka kerja pengendalian impedansi hibrida, dapat memberikan pengaturan torsi dan ketahanan sistem yang unggul. [ 13 ] Namun, mengoptimalkan pengendali ini merupakan tantangan karena kendala nonlinier berdimensi tinggi.
Untuk mengatasi tantangan ini, particle swarm optimization (PSO) telah banyak digunakan sebagai teknik optimasi yang efisien untuk menyetel parameter FH-IC. [ 14 – 16 ] PSO menunjukkan konvergensi yang cepat dan kemampuan beradaptasi yang kuat, sehingga sangat cocok untuk optimasi kontrol waktu nyata. [ 17 ]
Di luar kendali impedansi hibrida konvensional, kendali impedansi hibrida adaptif (AHIC) telah muncul sebagai kerangka kerja kendali canggih yang menyesuaikan parameter kendali secara dinamis sebagai respons terhadap variasi lingkungan. Studi telah menunjukkan bahwa AHIC menawarkan pelacakan lintasan dan penolakan gangguan yang lebih baik dalam aplikasi robotik:
Chen et al. mengusulkan pengontrol RSEA berbasis AHIC yang mengintegrasikan kontrol impedansi turunan integral proporsional dengan kontrol adaptif referensi model, yang menunjukkan akurasi pelacakan dan penolakan gangguan yang tinggi. [ 18 ] Hongli et al. mengembangkan pengontrol impedansi hibrida adaptif dinamis, yang menunjukkan pelacakan gaya yang unggul dalam lingkungan yang dinamis. [ 19 ] Qian et al. merancang elemen elastis seri putar yang dapat dikonfigurasi ulang, yang menunjukkan pelacakan torsi yang ditingkatkan dalam aplikasi interaksi manusia-robot. [ 20 ] Wang et al. memperkenalkan aktuator kekakuan variabel yang ringan, yang mencapai rentang kekakuan yang luas (0–988 Nm rad −1 ) dengan bobot yang rendah (0,412 kg). [ 21 ] Liu et al. menerapkan AHIC ke rangka luar yang lentur, menggunakan pengatur kuadrat linier dan kontrol mode geser (SMC) untuk meningkatkan kekokohan dan pelacakan lintasan. [ 22 ]
Studi-studi ini menggambarkan semakin pentingnya kontrol impedansi hibrida adaptif dalam RSEA. Akan tetapi, metode yang ada masih menghadirkan tantangan terkait kemampuan adaptasi waktu nyata, penyetelan parameter, dan ketahanan dalam lingkungan yang kompleks, sehingga memerlukan penelitian lebih lanjut.
Studi ini mengusulkan strategi kontrol impedansi baru, yang disebut kontrol impedansi hibrid fraksional adaptif (AFH-IC), yang secara khusus dirancang untuk aktuator elastis seri putar (RSEA) yang beroperasi pada berbagai medan datar, di mana arsitektur kontrol mengintegrasikan kontrol orde fraksional untuk mencapai torsi yang presisi dan pengaturan posisi, logika fuzzy adaptif untuk menyetel parameter kontrol secara dinamis sebagai respons terhadap variasi lingkungan, dan PSO untuk penyesuaian parameter yang optimal, dengan tujuan keseluruhan untuk meminimalkan kelebihan torsi selama fase kontak sambil memastikan kinerja pelacakan gaya sensitivitas tinggi di lingkungan yang menantang seperti lantai padat, karpet, dan rumput, di mana metode kontrol tradisional sering kali gagal mempertahankan operasi yang stabil dan akurat.
Kontribusi dari karya ini ada tiga. Pertama, kerangka kerja kontrol adaptif berbasis logika fuzzy baru diusulkan, yang mampu menyetel parameter fraksional posisi dan kesalahan gaya secara real-time. Hal ini memungkinkan penggunaan energi yang efisien dan kepatuhan lingkungan yang dinamis. Sejauh pengetahuan kami, pendekatan ini belum pernah dilaporkan sebelumnya dalam literatur. Kedua, pegas datar torsional Fibonacci ganda yang dirancang khusus, dibuat dari titanium, diperkenalkan sebagai bagian dari sistem RSEA. Parameter pegas titanium dipilih secara optimal untuk mencapai kekakuan tinggi dan efisiensi mekanis. Ketiga, pendekatan fuzzy orde fraksional memungkinkan pengoptimalan parameter kontrol secara real-time, yang memungkinkan struktur kontrol sistem RSEA untuk secara efektif beradaptasi dengan perubahan disruptif eksternal.
Sisa artikel ini disusun sebagai berikut. Bagian 2 memperkenalkan pemodelan matematika RSEA. Bagian 3 merinci analisis stabilitas FH-IC. Bagian 4 menjelaskan detail implementasi AFH-IC yang diusulkan. Bagian 5 menyajikan hasil eksperimen dan simulasi. Terakhir, Bagian 6 diakhiri dengan ringkasan temuan dan pembahasan arah penelitian mendatang.
2 Deskripsi dan Pemodelan Sistem
Pada bagian ini, desain mekanis pegas datar titanium, pemodelan dinamis RSEA, dan pengaturan eksperimen yang digunakan dalam penelitian ini dijelaskan secara rinci.
2.1 Deskripsi Sistem
Gambar 1 menunjukkan struktur yang dikendarai oleh RSEA dengan beban. Susunan percobaan dirancang berdasarkan batas gaya atas pergelangan kaki manusia. Aktuator terdiri dari beberapa komponen, termasuk roda gigi cacing, motor servo, pegas datar torsional Fibonacci ganda (DFTFS), encoder inkremental, penghubung beban, dan sambungan putar, seperti yang ditunjukkan pada Gambar 2 .
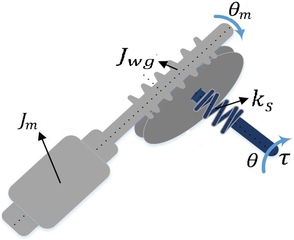

Untuk mengukur torsi keluaran, transduser torsi putar (TRS600 50 Nm FUTEK) dengan sensitivitas 0,01 Nm diintegrasikan ke dalam platform. Selain itu, motor servo (LFTM-50) digunakan untuk menggerakkan sistem. Roda gigi cacing mengubah gerakan rotasi motor sepanjang sumbu x menjadi gerakan rotasi sepanjang sumbu y sekaligus mengurangi kecepatan rotasi. Komponen roda gigi cacing dihubungkan ke DFTFS, yang mentransmisikan torsi ke poros beban akhir, sementara komponen cacing secara langsung dikopel ke poros motor.
Bahan pegas di sini digunakan sebagai Titanium (Ti-Grade 2). Dalam kondisi pembebanan normal, kekakuannya menunjukkan perilaku linier hingga lilitan mencapai titik kontak, seperti yang diilustrasikan pada Gambar 3. Konstanta kekakuan pegas adalah 76,305 Nm rad −1 .
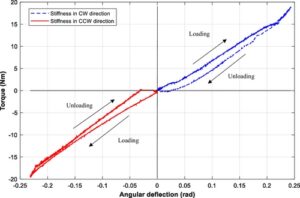
Roda gigi cacing, seperti yang digambarkan pada Gambar 4 , memiliki rasio transmisi 1:60 dalam sistem RSEA. Posisi poros motor diukur menggunakan encoder inkremental 10-bit, sementara posisi beban juga dipantau melalui encoder inkremental 10-bit yang terpasang pada roda gigi cacing. [ 23 ] Perbedaan sudut antara poros motor dan beban dihitung untuk menentukan deformasi pegas.

Massa efektif pegas di RSEA jauh lebih rendah daripada massa efektif motor dan kotak roda gigi, serta inersia kotak roda gigi. Oleh karena itu, efek pegas aktuator elastis dapat dianggap sebagai pegas tanpa massa, terutama saat menggunakan motor dengan rasio roda gigi tinggi. Sebaliknya, massa efektif tautan umumnya sedikit lebih tinggi.
2.2 Pemodelan RSEA
Gambar 4 mengilustrasikan komponen terperinci dari sistem RSEA. Motor servo dengan kotak roda gigi cacing digunakan untuk menerapkan gaya pada DFTFS di RSEA. Selain itu, dua encoder inkremental digunakan untuk mengukur sudut poros motor ( θ m ) dan sudut sambungan beban ( θ ).
Untuk meniru kondisi lingkungan dunia nyata secara akurat, pengaturan eksperimen menggunakan tiga permukaan berbeda: lantai padat (kondisi keras), karpet (kondisi sedang), dan rumput (kondisi lunak).
Permukaan ini dipilih untuk mensimulasikan berbagai tingkat kepatuhan, memastikan bahwa kemampuan beradaptasi dan kekokohan pengontrol dapat diuji dalam kondisi kekakuan yang berbeda.
Dalam model torsi eksperimental RSEA, posisi motor dan beban dapat diukur secara langsung. [ 11 ] Namun, untuk mengembangkan model torsi yang akurat, koefisien gesekan pada sambungan beban sistem harus diperkirakan secara eksperimental (lihat Tabel 1 ).
| Parameter | Simbol | Nilai rata-rata |
|---|---|---|
| Torsi RSEA maksimum | τmax | 26 juta ton |
| Deformasi DFTFS maksimum | Δθ | 0,25 rad |
| Koefisien redaman total di RSEA | Btot | 0,183 kgm2 detik −1 |
| Inersia rotasi total di RSEA | Jtot | 2.3208 kgm2 detik -1 |
| Momen inersia motor | Jm | 0,00024 kgm −2 |
| Momen inersia roda cacing | Jwg | 0,000392 kgm −2 |
| Kekakuan DFTFS | ks | 76,305 N.m rad −1 |
| Rasio roda cacing | N | 60 |
| Panjang tautan beban | lr | 0,3 juta |
Pegas elastis seri dalam sistem kontrol loop tertutup berfungsi sebagai aktuator dan transduser. Karena pegas diposisikan di antara beban dan motor, torsi ditransmisikan melalui struktur elastis. Sementara itu, torsi yang ditransmisikan dapat ditentukan dengan mengukur deformasi pegas. Selama percobaan, sistem dipasang pada alas tetap, dan interaksi torsi dengan setiap permukaan dianalisis untuk mengevaluasi efektivitas pendekatan AFH-IC. Hasil percobaan menunjukkan bahwa pengontrol berhasil beradaptasi dengan kondisi lingkungan yang berbeda, mempertahankan torsi dan kontrol posisi yang stabil meskipun ada variasi dalam kekakuan permukaan.
Model dinamis numerik RSEA telah dikembangkan menggunakan kotak peralatan Matlab/Simscape, yang memungkinkan perbandingan dengan model matematika analitis. Model RSEA Matlab/Simscape diilustrasikan dalam Gambar 5a , sementara Gambar 5b menunjukkan berbagai tampilan model solid 3D dalam Matlab/Simulink. Dalam sistem yang disimulasikan, posisi beban berkurang karena berat beban, yang mengarah ke keadaan yang tidak terkendali. Selain itu, torsi beban tanpa adanya kontrol torsi umpan balik bervariasi karena perubahan gaya gravitasi, yang mencegah pengontrol mempertahankan lintasan yang diinginkan.
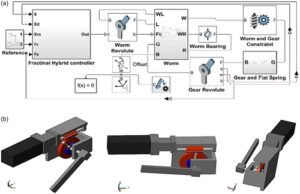
Dalam aplikasi dunia nyata, jika kekakuan DFTFS ditetapkan terlalu rendah, torsi motor menjadi jenuh, dan lebar pita kontrol torsi loop terbuka menurun, yang berdampak negatif pada kinerja sistem.
3 Model Kontrol Impedansi Hibrida Fraksional
MJ Fotuhi et al. [ 8 ] mengembangkan pendekatan FH-IC untuk kontrol pelacakan torsi yang sangat sensitif dari RSEA di lingkungan yang tidak pasti. Rincian lebih lanjut tentang model FH-IC dapat ditemukan dalam ref. [ 24 ]. Parameter fraksional FH-IC dioptimalkan menggunakan algoritma PSO di bawah tiga mode operasi yang berbeda. Model ini dioptimalkan berdasarkan data posisi dan torsi eksperimental, yang menunjukkan kemampuan beradaptasi yang unggul terhadap tekanan lengan di lingkungan eksperimental nyata, seperti lantai padat (keras), karpet (sedang), dan rumput (lunak), dibandingkan dengan kontrol impedansi konvensional.
Kerangka kerja H-IC mencakup kontrol impedansi berbasis gaya dan kontrol impedansi berbasis posisi, dengan parameter pembobotan. [ 19 , 20 ] Nilai w yang dapat diterima di bawah ini berada dalam kisaran [0,1]. Persamaan kontrol untuk FH-IC didefinisikan sebagai
![]()


di mana N adalah jumlah total sampel. Proses optimasi FH-IC dijalankan secara iteratif menggunakan PSO, dengan parameter diperbarui pada setiap siklus simulasi.
Parameter algoritma PSO untuk menyetel koefisien pengontrol dirangkum dalam Tabel 2. Pada generasi pertama, nilai acak awal partikel dihasilkan berdasarkan distribusi probabilistik yang telah ditentukan sebelumnya. Karena sifat probabilistik dari proses pencarian, PSO dijalankan beberapa kali untuk memperoleh nilai koefisien yang optimal.
| Parameter | Nilai |
|---|---|
| Ukuran populasi (P) | 15 |
| Nomor partikel | 10 |
| Batas bawah [k0,kp0,α0,β0,γ0] | [0,0,0,0,0] |
| Batas atas [kv0,kp0,α0,β0,γ0] | [1,1,1,100,100] |
| Batas bawah [kv1,kp1,α1,β1,γ1] | [0,0,0,0,0] |
| Batas atas [kv1,kp1,α1,β1,γ1] | [1,1,1,100,100] |
Dibandingkan dengan kontrol impedansi tradisional, pendekatan fuzzy orde fraksional yang diusulkan memberikan kemampuan beradaptasi yang unggul dengan meminimalkan kesalahan pelacakan dan mengoptimalkan parameter kontrol secara real time.
Tabel 3 merangkum parameter pengontrol FH-IC yang dioptimalkan untuk tiga gaya konstan yang berbeda dalam tiga lingkungan eksperimen nyata yang berbeda seperti lantai padat (keras), karpet (sedang), dan rumput (lunak). Hasil eksperimen menunjukkan bahwa FH-IC yang disetel secara fuzzy secara signifikan mengurangi kesalahan pelacakan torsi di berbagai tingkat kekakuan, sehingga meningkatkan stabilitas interaksi gaya.
| Parameter FH-IC | SFTPSO | MDMPSO | HRDPSO | Satuan |
|---|---|---|---|---|
| kv0 | 1.8720 | 2.7230 | 2.9519 | Nm/s rad -1 |
| kp0 | 12.1635 | 12.9410 | 14.2913 | Nm rad -1 |
| kv1 | 1.4613 | 2.5472 | 3.2624 | Nm/s rad -1 |
| kp1 | 11.4217 | 12.6720 | 14.1358 | Nm rad -1 |
| α0 | 0,5821 tahun | 0.6249 | 0.6650 | – |
| β0 | 0.7508 | 0,7939 | 0.8142 | – |
| γ0 | 0.7958 | 0.7944 | 0.7891 | – |
| α1 | 0.6824 | 0.7079 | 0.7031 | – |
| β1 | 0.6512 | 0.6814 | 0.8016 | – |
| γ1 | 0.6910 | 0.7392 | 0.7250 | – |
Persamaan dinamis kontrol impedansi dapat dirumuskan sebagai berikut:

Dalam stabilitas, salah satu isu krusial adalah bagaimana mengkonvergensikan kesalahan torsi e ke nol dalam rentang yang diinginkan. [ 29 ] Dengan menggabungkan Persamaan ( 8 ), ( 10 ), dan ( 11 ), Persamaan ( 12 ) dapat ditulis ulang menjadi

4 Implementasi Model Kontrol Impedansi Hibrida Fraksional Adaptif
Penelitian ini menyajikan pengembangan sistem inferensi logika fuzzy untuk memperkirakan koefisien fraksional dalam pengontrol impedansi adaptif RSEA. [ 31 ] Dalam kerangka H-IC, yang menggabungkan pengontrol torsi dan posisi, pengontrol logika fuzzy (FLC) diimplementasikan untuk menentukan koefisien fraksional secara dinamis. [ 32 ]
4.1 Perbandingan dengan Metode Kontrol Lanjutan Lainnya
Untuk menilai lebih lanjut efisiensi komputasi dan penerapan AFH-IC secara real-time, kami membandingkannya dengan teknik kontrol canggih lainnya seperti kontrol prediktif model (MPC) dan SMC.
4.1.1 Efisiensi Komputasi
MPC dikenal karena kompleksitas komputasinya yang tinggi karena pengoptimalan waktu nyata, sehingga menjadi tantangan bagi sistem dengan daya pemrosesan terbatas. SMC, meskipun tangguh, memerlukan peralihan frekuensi tinggi, yang meningkatkan beban komputasi. Sebaliknya, AFH-IC memanfaatkan logika fuzzy adaptif dengan kontrol orde fraksional, yang memungkinkan komputasi waktu nyata yang efisien tanpa tuntutan pemrosesan yang berlebihan.
Performa Waktu Nyata
Tidak seperti MPC, yang mengandalkan pengoptimalan berulang pada setiap langkah kontrol, AFH-IC secara dinamis menyesuaikan parameter impedansi menggunakan inferensi fuzzy, sehingga memberikan waktu respons yang lebih cepat dalam aplikasi dunia nyata. Dibandingkan dengan SMC, AFH-IC menunjukkan perilaku kontrol yang lebih halus dengan mengurangi efek getaran sekaligus menjaga stabilitas.
4.1.2 Kemampuan Beradaptasi terhadap Variasi Lingkungan
AFH-IC mengadaptasi parameter impedansi berdasarkan kondisi lingkungan (misalnya, permukaan keras, sedang, lunak), sedangkan MPC dan SMC memerlukan pemodelan eksplisit dari variasi tersebut, sehingga meningkatkan kompleksitas dan membatasi kemampuan beradaptasi di lingkungan yang tidak diketahui.
Secara keseluruhan, AFH-IC menawarkan alternatif yang efisien secara komputasi dan adaptif untuk MPC dan SMC, membuatnya sangat cocok untuk aplikasi kontrol torsi dan posisi waktu nyata dalam aktuator robotik.
FLC menerima dua masukan:
(koefisien elastis) dan turunannya
Proses pengembangan sistem FLC mencakup langkah-langkah kunci fuzzifikasi, defuzzifikasi, dan formulasi aturan. Variabel input
dan k ed dikategorikan ke dalam variabel linguistik, mulai dari tingkat kekerasan sangat rendah (VLH) hingga tingkat kekerasan sangat tinggi (VHH). Variabel keluaran, yang mewakili koefisien fraksional, ditetapkan ke himpunan fuzzy dengan istilah linguistik, termasuk sangat lunak (VST), lunak (SFT), sedang (MDM), keras (HRD), dan sangat keras (VHD).
Sistem RSEA menunjukkan nilai absolut maksimum
(koefisien elastis) dan k ed pada 50 dan 100 Nm s rad −1 , masing-masing. Rentang variabel input dan fungsi keanggotaan ditetapkan menggunakan data eksperimen untuk klasifikasi
dan k ed . Lebih jauh, fungsi keanggotaan ini ditentukan berkenaan dengan koefisien fraksional dari model estimasi fraksional adaptif (AF-EM), seperti yang dirinci dalam Tabel 3 .
Aspek penting dari metode ini adalah formulasi aturan fuzzy, yang secara signifikan mempengaruhi hasil keluaran. Aturan-aturan ini diturunkan dengan menggabungkan pengetahuan eksperimental
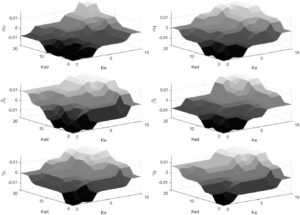
dan dikaitkan dengan hasil teoritis dari AF-EM untuk setiap kelas. [ 33 ] Fungsi keanggotaan Gaussian digunakan untuk memvisualisasikan variabel input dan output. Gambar 6 mengilustrasikan fungsi keanggotaan model impedansi fraksional adaptif (AFH-IM) yang digunakan dalam sistem RSEA.
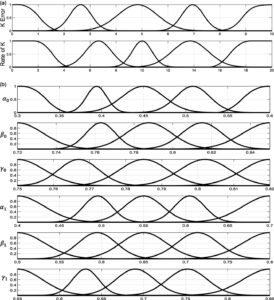
Dalam konteks RSEA, aturan fuzzy didefinisikan menggunakan format standar “IF-THEN”. Seperangkat aturan dibuat berdasarkan variabel output (koefisien fraksional) dan variabel input (
Dan
). Sebagai contoh, aturan fuzzy spesifik untuk
diberikan dalam Tabel 4 , yang mewakili salah satu dari enam parameter yang digunakan dalam sistem logika fuzzy. Aturan FLC untuk model estimasi fraksional adaptif berasal dari hasil eksperimen yang dikumpulkan untuk pelacakan torsi dan posisi dalam sistem RSEA.
| k e k ed | VLH | LHN | MHN | HHN | VHH |
|---|---|---|---|---|---|
| VLH | VST | VST | Bahasa Indonesia: SFT | Bahasa Indonesia: SFT | MDM |
| LHN | VST | VST | Bahasa Indonesia: SFT | Bahasa Indonesia: SFT | MDM |
| MHN | VST | Bahasa Indonesia: SFT | Bahasa Indonesia: SFT | MDM | SDM |
| HHN | Bahasa Indonesia: SFT | Bahasa Indonesia: SFT | MDM | SDM | SDM |
| Bahasa Inggris VHN | Bahasa Indonesia: SFT | MDM | MDM | SDM | Video dalam format VHD |
Defuzzifikasi mengubah nilai fuzzy menjadi keluaran numerik yang jelas. Dalam penelitian ini, metode centroid digunakan untuk defuzzifikasi.
Gambar 7 memberikan representasi visual dari permukaan FLC, mengilustrasikan hubungan antara
dan k ed output fuzzy dari koefisien fraksional dalam AFH-IM. Representasi grafis ini meningkatkan pemahaman tentang bagaimana FLC mengubah data input fuzzy menjadi nilai output yang tepat dan dapat ditindaklanjuti.
5 Hasil Simulasi dan Eksperimen
Bagian ini memverifikasi keakuratan, penerapan, dan inovasi metode yang diusulkan melalui beberapa simulasi dan eksperimen. Hasil simulasi di sini pertama-tama memverifikasi penerapan dan keandalannya, kemudian eksperimen dilakukan untuk memverifikasi lebih lanjut hasil ini. Model eksperimen RSEA dikembangkan untuk mengevaluasi kinerja AFH-IC dengan pegas datar titanium. Dalam pengaturan eksperimen, sistem RSEA dipasang pada alas tetap untuk melakukan gerakan sendi lengan dalam tiga kondisi lingkungan: keras, sedang, dan lunak. Bagian ini menyajikan hasil simulasi dan eksperimen pengaturan RSEA dalam tiga mode pengontrol yang berbeda.
Torsi keluaran sistem diperoleh dari dua sumber: pengukuran eksperimental menggunakan sensor torsi yang dipasang dalam sistem dan simulasi berdasarkan model torsi matematika.
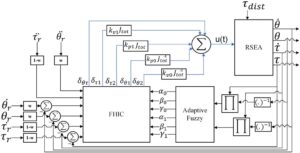
Pendekatan sumber data ganda ini digunakan untuk memungkinkan perbandingan kinerja yang komprehensif dari sambungan beban. Gambar 8 mengilustrasikan struktur pengontrol impedansi hibrida fraksional adaptif (AFHI), yang memproses beberapa parameter masukan, termasuk kesalahan posisi, kesalahan torsi (selisih antara torsi yang diinginkan dan aktual), posisi umpan balik, dan torsi lingkungan yang diterapkan tegak lurus ke tautan. Berdasarkan masukan ini, pengontrol AFHI menghasilkan sinyal kontrol yang dikirimkan ke sistem RSEA untuk menyesuaikan posisinya dan mempertahankan gaya konstan atau mencapai tujuan kontrol yang diinginkan. Untuk menilai lebih lanjut kekokohan pengontrol AFHI, sensitivitasnya terhadap parameter fraksional dievaluasi, bersama dengan kemampuannya untuk menangani gangguan eksternal dan variasi parameter di berbagai kondisi lingkungan.
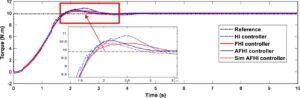
Bahasa Indonesia: Di bagian ini, kami mengevaluasi kinerja pelacakan lintasan dinamis dari strategi AFH-IC yang diusulkan. Seperti yang ditunjukkan pada Gambar 9-11 , metode AFH – IC menunjukkan peningkatan substansial dalam pelacakan torsi dinamis dibandingkan dengan pendekatan HI dan FH-IC. Secara khusus, kesalahan pelacakan rotasi maksimum berkurang dari 3,83 menjadi 0,59 Nm s −1 . Nilai akar rata-rata kuadrat (RMS) dari kesalahan torsi berkurang dari 1,93 menjadi 0,63 Nm s −1 . Sistem logika fuzzy adaptif dalam AFH-IC secara dinamis menyesuaikan parameter fraksional ( α , β , γ ) untuk mempertahankan ketahanan dan secara efektif mengompensasi gangguan eksternal, dengan demikian meningkatkan stabilitas sistem di berbagai medan. Penting untuk dicatat bahwa beberapa fluktuasi dalam torsi yang dikendalikan selama interaksi dengan lingkungan dapat dikaitkan dengan kekasaran permukaan kontak, yang membuatnya sulit untuk menghilangkan variasi ini sepenuhnya. Meskipun demikian, nilai torsi umumnya tetap berpusat di sekitar titik setel 10 Nm. Hasil eksperimen dengan jelas menunjukkan bahwa desain dan penerapan pendekatan AFH-IC secara signifikan meningkatkan kinerja pelacakan torsi dinamis, menjadikannya strategi yang menjanjikan untuk mencapai kontrol torsi yang tepat dan stabil dalam skenario pelacakan lintasan dinamis.

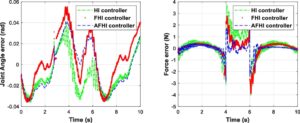
Gambar 12 mengilustrasikan perilaku dinamis parameter fraksional (
) yang diperoleh oleh model fuzzy adaptif untuk FH-IC dari sistem RSEA. Seperti yang dapat dilihat dari Gambar 11 dan 12 , hasil eksperimen yang diperoleh di sini mendekati hasil simulasi dan Kinerja kesalahan eksperimen menunjukkan bahwa model AFH-IC mempertahankan kesalahan pelacakan yang lebih rendah, yang menunjukkan ketahanannya yang unggul terhadap variasi parameter.

Gambar 13 menggambarkan parameter fraksional yang diperoleh oleh model fuzzy adaptif untuk FH-IC dari sistem RSEA selama perubahan mode beban eksternal. Selama percobaan, mode beban eksternal dialihkan dari mode sedang ke mode keras, di mana torsi mencapai kondisi stabil antara 4 dan 5 detik. Kemudian, mode beban eksternal dialihkan ke mode lunak setelah 6 detik; mode sedang, keras, dan lunak selanjutnya diterapkan secara berurutan. Hasil percobaan menyoroti bahwa AFH-IC secara efektif mengompensasi gangguan eksternal dan mempertahankan stabilitas torsi, bahkan dalam kondisi lingkungan yang bervariasi.
Untuk mengevaluasi kinerja pengendali FHI-SFT PSO , FHI-MDM PSO , dan FHI-HRD PSO , pengendali HI, dan
, RMSE posisi dan torsi (RMSE P dan RMSE F ) antara sinyal terukur dari sambungan beban dan sinyal referensi dihitung berdasarkan Persamaan ( 7 ). Tabel 5 memberikan RMSE terhitung untuk semua pengendali yang dikembangkan di sini. Berdasarkan RMSE yang diperoleh,
kuat terhadap gangguan dan menghasilkan RMSE terbaik dibandingkan pengontrol lainnya.
| Tipe pengontrol | Nilai RMSE P (rad) | Nilai RMSE (Nm) |
|---|---|---|
| HI | 0.23821 | 0,58727 tahun |
| PSO FHI-SFT | 0.19264 | 0.42793 |
| PSO FHI-MDM | 0.20486 | 0,54835 tahun |
| FHI-HRD PSO | 0.23715 | 0.58321 |
| AFHI | 0.18417 | 0.37423 |
Berdasarkan hasil pada Tabel 6 , temuan ini menegaskan bahwa AFH-IC mengungguli pengontrol HI dan FH-IC dalam pengendalian impedansi sistem RSEA dengan memberikan ketahanan yang lebih besar terhadap variasi parameter dan gangguan lingkungan.
| Tipe pengontrol | Tingkat RMSE P | Tingkat F RMSE |
|---|---|---|
| AFHImelawanHI | 11,38% | 18,15% |
| AFHI versus FHI-SFT PSO | 6,84% | 12,37% |
| AFHI versus PSO FHI- MDM | 6,03% | 9,26% |
| AFHI versus FHI-HRD PSO | 7,55% | 15,54% |
| PSO FHI-MDM versus HI | 8,46% | 13,51% |
| PSO FHI-MDM versus PSO FHI-SFT | 6,17% | 10,80% |
| PSO FHI-MDM versus PSO FHI-HRD | 7,25% dari total | 12,72% |
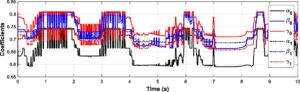
Temuan ini menunjukkan bahwa pengontrol PSO FHI-MDM bekerja lebih akurat daripada pengontrol HI dan pengontrol FHI lainnya , khususnya dalam aplikasi kontrol impedansi untuk sistem RSEA. Variasi parameter fraksional ( α0 , β0 , γ0 , α1 , β1 , γ1 ) dari A-FH-IC dalam menanggapi masukan sinusoidal ditunjukkan pada Gambar 14. Dalam percobaan ini , terlihat dalam rentang mana dan bagaimana parameter fraksional berubah secara adaptif terhadap efek gangguan.
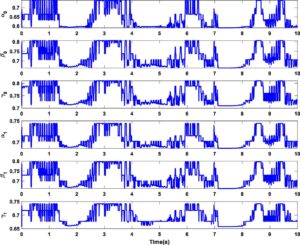
Dalam hal RMSEP (root mean square error of position), pengendali HI mencapai peningkatan sebesar 11,38%, sedangkan pengendali FHI-SFT PSO , FHI-MDM PSO , dan FHI-HRD PSO menunjukkan peningkatan masing-masing sebesar 6,84, 6,03, dan 7,55%. Demikian pula, untuk RMSEF (root mean square error of force), pengendali HI mencapai peningkatan sebesar 18,15%, sedangkan pengendali FHI-SFT PSO , FHI-MDM PSO , dan FHI-HRD PSO menunjukkan peningkatan masing-masing sebesar 12,37, 9,26, dan 15,54%.
Lebih jauh lagi, ketika secara khusus membandingkan pengontrol PSO FHI-MDM , pengontrol ini terbukti berkinerja lebih akurat daripada pengontrol HI dan pengontrol FHI lainnya untuk kontrol impedansi RSEA. Peningkatan yang diamati adalah:
Dalam hal RMSEP, pengendali HI, FHI-SFT PSO , dan FHI-HRD PSO masing-masing mencapai peningkatan sebesar 8,46, 6,17, dan 7,25%. Mengenai RMSEF, pengendali yang sama menunjukkan peningkatan masing-masing sebesar 13,51, 10,80, dan 12,72%.
Temuan ini menunjukkan bahwa pengontrol PSO FHI-MDM sangat efektif dalam meningkatkan kinerja kontrol impedansi untuk sistem RSEA dibandingkan dengan pengontrol HI dan pengontrol FHI lainnya.
6 Keterbatasan dan Pekerjaan Masa Depan
Walaupun model AFH-IC yang diusulkan telah menunjukkan keuntungan signifikan dalam hal efisiensi komputasi, ketahanan, dan kemampuan beradaptasi, masih ada beberapa keterbatasan yang harus diatasi dalam penelitian masa mendatang.
Meskipun kerangka kerja AFH-IC menunjukkan efisiensi komputasi yang lebih tinggi dibandingkan dengan pendekatan tradisional seperti MPC dan SMC, implementasi real-time-nya masih menuntut keseimbangan antara akurasi dan kapasitas pemrosesan, khususnya dalam aplikasi dengan kendala temporal yang ketat, yang mungkin memerlukan strategi optimasi tambahan, sementara validasi saat ini pada aktuator derajat kebebasan tunggal (DOF) membatasi skalabilitasnya pada sistem multi-DOF, sehingga memerlukan modifikasi lebih lanjut dalam arsitektur kontrol dan alokasi sumber daya, dan meskipun integrasi logika fuzzy meningkatkan kemampuan beradaptasi sistem, ia juga memperkenalkan tantangan penyetelan parameter yang dapat diatasi melalui metode optimasi otomatis seperti pembelajaran penguatan atau algoritma metaheuristik, sedangkan sensitivitasnya terhadap variabilitas lingkungan—meskipun kemampuan beradaptasi yang ditunjukkan pada permukaan dengan kekakuan yang bervariasi—tetap menjadi kendala dalam kondisi yang sangat dinamis atau tidak terstruktur, yang menunjukkan perlunya validasi eksperimental yang lebih luas.
Dalam penelitian mendatang, pendekatan AFH-IC diharapkan dapat diperluas ke platform robotik multi-DOF seperti lengan yang diartikulasikan dan rangka luar, yang akan melibatkan upaya memastikan kelayakan waktu nyata dan stabilitas sistem, sementara penggunaan teknik akselerasi perangkat keras, termasuk array gerbang yang dapat diprogram di lapangan atau komputasi berbasis GPU, dapat mengurangi latensi pemrosesan secara signifikan, dan penggabungan teknik berbasis pembelajaran adaptif—seperti jaringan saraf atau algoritma pembelajaran penguatan—dapat meningkatkan kemampuan penyetelan otonom pengontrol, sehingga mengurangi ketergantungan pada penyetelan manual, sedangkan pengujian di dunia nyata dalam lingkungan yang kompleks dan dinamis, termasuk skenario interaksi manusia-robot dan pergerakan medan yang tidak rata, akan sangat penting untuk menilai kekokohan, kepraktisan, dan skalabilitas metode yang diusulkan.
7 Kesimpulan
Studi ini menyajikan desain, implementasi, dan evaluasi strategi AFH-IC baru untuk RSEA, yang ditujukan untuk meningkatkan akurasi pelacakan torsi, ketahanan, dan kemampuan beradaptasi dalam lingkungan yang tidak pasti dan dinamis. Metode yang diusulkan mengintegrasikan kontrol orde fraksional dengan logika fuzzy adaptif dan diuji melalui simulasi dan eksperimen waktu nyata menggunakan Papan Pengontrol R&D DS1104. DFTFS yang dirancang khusus dimasukkan sebagai penyangga energi, dan estimasi torsi yang tepat dicapai melalui defleksi pegas di bawah kontrol impedansi. Untuk menilai kinerja pengontrol secara sistematis di berbagai interaksi lingkungan, tiga mode gaya kontak didefinisikan dan diuji, yaitu, PSO FHI-SFT (lunak), PSO FHI-MDM (sedang), dan PSO FHI-HRD (keras).
Pengendali AFH-IC menunjukkan kinerja unggul baik dalam hal akurasi pelacakan posisi maupun torsi, mencapai pengurangan RMSEP sebesar 11,38% dibandingkan dengan pengendali HI dan 6,03% dibandingkan dengan pengendali FH-IC, sementara juga memperoleh peningkatan RMSEF sebesar 18,15% dibandingkan dengan pengendali HI dan 9,26% dibandingkan dengan pengendali FH-IC, dengan demikian menegaskan efektivitasnya dalam mengurangi kesalahan impedansi pada berbagai kondisi kontak.
Sebagai kesimpulan, kerangka kerja AFH-IC yang diusulkan menawarkan solusi kontrol yang andal, fleksibel, dan berkinerja tinggi untuk sistem interaksi manusia-robot, khususnya dalam skenario yang melibatkan medan variabel dan kondisi beban nonlinier. Struktur adaptifnya menghilangkan kebutuhan untuk penyetelan manual atau kustomisasi individual, dan implementasinya yang berhasil memberikan landasan yang kuat untuk pengembangan pengontrol impedansi yang dapat diskalakan dan mendukung pembelajaran dalam platform robotik generasi berikutnya.
