Abstrak
Simulasi kerumunan yang dapat dipercaya untuk aplikasi seperti film atau permainan merupakan tantangan karena banyaknya komponen yang menyusun hasil yang realistis. Pengguna biasanya perlu menyetel sejumlah besar parameter simulasi secara manual hingga mencapai hasil yang diinginkan. Kami memperkenalkan MPACT , sebuah kerangka kerja yang memanfaatkan pengodean berbasis gambar untuk mengubah data kerumunan yang tidak berlabel menjadi parameter yang bermakna dan dapat dikontrol untuk pembuatan kerumunan. Intinya, kami melatih jaringan prediksi parameter pada serangkaian data sintetis yang beragam, yang mencakup pasangan gambar dan profil kerumunan yang sesuai. Ruang parameter yang dipelajari memungkinkan: (a) penulisan dan kontrol kerumunan secara implisit, yang memungkinkan pengguna untuk menentukan skenario kerumunan yang diinginkan menggunakan data lintasan dunia nyata, dan (b) analisis kerumunan, yang memfasilitasi identifikasi perilaku kerumunan dalam input dan klasifikasi skenario yang tidak terlihat melalui operasi dalam ruang laten. Kami mengevaluasi kerangka kerja kami secara kuantitatif dan kualitatif, membandingkannya dengan data dunia nyata dan garis dasar yang dipilih, sambil juga melakukan studi pengguna dengan pengguna ahli dan pemula. Eksperimen kami menunjukkan bahwa kerumunan yang dihasilkan mendapat skor tinggi dalam hal kepercayaan simulasi, keplausifan, dan kesetiaan perilaku kerumunan.
1 Pendahuluan
Simulasi gerakan merupakan bagian penting dalam menciptakan dunia virtual yang padat dan berkualitas tinggi. Simulasi yang masuk akal sangat penting untuk persepsi realisme adegan film dan lingkungan permainan video, serta keberhasilan sistem perencanaan kota, evakuasi, dan visualisasi arsitektur. Dengan demikian, tujuan dalam domain simulasi kerumunan adalah untuk menciptakan kerumunan virtual yang bergerak dan berinteraksi secara realistis dan alami dengan mudah, intuitif, dan cepat.
Sebelumnya, penelitian di bidang ini terutama menekankan tugas-tugas dasar pencarian tujuan dan penghindaran tabrakan, yang telah ditingkatkan secara progresif selama bertahun-tahun [ VTP21 ]. Baru-baru ini, fokus bergeser ke diversifikasi kerumunan dengan mengintegrasikan perilaku yang lebih canggih, lebih dekat dengan yang diamati di dunia nyata. Kami mencatat bahwa ‘perilaku’ kerumunan mengacu pada gerakan lokal agen dalam jendela waktu, misalnya, percakapan stasioner yang kemudian dapat beralih menjadi meninggalkan kelompok. Pergeseran ini mengarah pada studi tentang pembentukan kelompok, perilaku statis yang lebih kompleks, dan interaksi agen dengan elemen lingkungan, seperti titik-titik minat (POI) [ TYK*09 , KBK16 ]. Namun, pada kenyataannya, orang sering melakukan beberapa tugas navigasi secara bersamaan alih-alih berurutan. Menangkap kompleksitas ini tidak hanya memerlukan pemodelan gerakan individu, tetapi juga secara akurat mewakili interaksi rumit di antara mereka dalam konteks lingkungan. Metode berbasis data dan pembelajaran menunjukkan janji untuk usaha semacam itu, namun, mereka sangat dibatasi oleh data masukan. Selain itu, model perilaku yang dipelajari terkadang diperlakukan sebagai informasi kotak hitam tanpa parameterisasi, sehingga membatasi kebebasan kreatif penulis [ LCL07 , CPV*23 ].
Kompleksitas simulator pada akhirnya bergantung pada sifat parameter yang disertakannya. Sebagian besar kerangka kerja bergantung pada pemilihan parameter simulator secara manual, yang sering kali memakan waktu, bias pengguna, memerlukan pengetahuan ahli atau eksperimen coba-coba yang membosankan. Tak pelak, hal ini membuka jalan bagi kategori penelitian baru yang didedikasikan untuk mengoptimalkan parameter simulator. Sejauh ini, metode pengoptimalan terbatas untuk menangani sebagian besar parameter navigasi/pengarahan, seperti penyimpangan jalur dan kecepatan, jarak interpersonal dan kepadatan [ WJGO*14 , KSHG18 ], dan bukan variabel perilaku tingkat tinggi. Secara keseluruhan, mencapai kerumunan yang autentik dan meyakinkan bergantung pada ekspresi parameter simulator dan bagaimana nilainya dipilih ; simulasi sama bagusnya dengan pilihan nilai parameter kontrol.
Menentukan nilai parameter secara manual sering kali menyiratkan adanya trade-off antara kemudahan penggunaan dan tingkat realisme yang dicapai. Alat yang lebih intuitif menyediakan kontrol makroskopis, misalnya, aliran dan kepadatan, tetapi mencapai individualitas sering kali mustahil, atau memerlukan penyetelan manual yang ekstensif. Selain itu, meskipun berbagai antarmuka pengguna (UI) telah dirancang untuk menyediakan kontrol intuitif bagi pengguna, efektivitasnya bergantung pada seberapa mudah pengguna memahami efek perubahan parameter simulasi pada pembuatan. UI yang mudah digunakan, yang mengintegrasikan kemampuan kerangka kerja simulasi yang kompleks secara mulus, memaksimalkan kegunaan tidak hanya bagi pengguna pemula tetapi juga bagi profesional industri.
Tujuan kami adalah untuk memberikan kerangka kerja komprehensif yang merepresentasikan data kerumunan yang tidak berlabel dengan cara yang bermakna dan terkendali, menerjemahkannya ke dalam parameter untuk model kerumunan. Secara khusus, kami mengembangkan alur inferensi (Gambar 2 ) yang pertama-tama mengambil data kerumunan yang sembarangan (lintasan) dan mengodekannya menggunakan representasi khusus dalam ruang gambar (Bagian 3.2 ); representasi ini ideal untuk mengodekan informasi spasial. Metode kami beroperasi secara mesoskopis – perspektif perantara antara mikroskopis (per-agen) dan makroskopis (kerumunan secara keseluruhan), dengan fokus pada area yang ditunjuk dalam suatu lingkungan selama interval waktu tertentu. Dengan demikian, metode kami adalah metode mesoskopis untuk membuat profil dan mengabstraksi lintasan kerumunan (MPACT) yang secara efektif mengabstraksikan perilaku yang ditemukan dalam data kerumunan.


Berikutnya, kami sampaikan sebuah model (Bagian 3.3 ), dilatih untuk menavigasi dari ruang representasi input (ruang gambar) ke ruang parameter simulator yang lebih padat dan dapat dijelaskan (ruang laten MPACT). Berdasarkan desainnya, model kami mengoptimalkan parameter simulator kerumunan yang mendasarinya (modCCP—versi CCP yang dimodifikasi [ PKL*22 ]) yang disajikan di Bagian 3.1 . Definisi parameter ini bersifat tingkat tinggi dan dapat ditafsirkan, dan kombinasinya mendefinisikan profil perilaku yang mampu menggambarkan berbagai tugas kerumunan (Gambar 1 ), menjadikannya metode yang dapat digunakan dan holistik. Kami mengeksplorasi ruang MPACT dan menunjukkan bagaimana kami dapat menggunakannya untuk membuat profil skenario yang tidak diketahui dan tidak terlihat, serta bagaimana kami mengoperasikannya, misalnya, interpolasi antara titik-titik di ruang ini menghasilkan simulasi yang masuk akal dan terkendali.
Kerangka kerja kami memungkinkan pengguna untuk memandu pembuatan secara implisit dengan memilih data kerumunan referensi. MPACT kemudian memprediksi parameter simulator, yang mencerminkan perilaku yang diamati dalam simulasi yang dihasilkan (Bagian 3.4 ). Ini menghilangkan kebutuhan untuk definisi perilaku eksplisit, menghindari eksperimen yang memakan waktu dan keahlian dalam dinamika kerumunan. Untuk skenario sederhana (misalnya, pengelompokan statis diikuti oleh pencarian tujuan), pengguna dapat mengandalkan modCCP atau simulator mapan lainnya. Namun, menangkap pola kerumunan dunia nyata yang rumit dengan perilaku kompleks merupakan tantangan dan tidak efisien melalui penyetelan manual. Model pengoptimalan kami secara otomatis membuat profil lintasan sambil memungkinkan penyetelan halus parameter yang dapat ditafsirkan, bila diperlukan.
Penting untuk dicatat bahwa sistem kami bukanlah metode optimasi untuk replikasi jalur; sebaliknya, kami fokus pada pencapaian kesamaan perilaku . Dua jalur mungkin bervariasi secara spasial tetapi memiliki maksud perilaku yang sama seperti bergerak ke kanan lalu mengelompokkan, atau ke kiri lalu mengelompokkan, keduanya mencerminkan tujuan pergerakan yang serupa. Setelah menerapkan model kami, pengguna dapat secara dinamis menyempurnakan profil yang diprediksi dan mendistribusikannya dalam lingkungan yang dibuat khusus melalui antarmuka kami yang intuitif dan ramah pengguna. Langkah terakhir melibatkan pembuatan simulasi kerumunan baru dengan mendefinisikan inisialisasi agen dan memungkinkan mereka untuk menavigasi menggunakan simulator yang mendasarinya, dipandu oleh parameter yang diprediksi MPACT.
Singkatnya, kami memperkenalkan kerangka kerja MPACT, yang mengekstrak parameter spesifik simulator spasio-temporal dengan mempelajari ruang laten terstruktur. Kontribusi utama kami adalah model prediktif yang memetakan data lintasan arbitrer ke parameter yang dapat dijelaskan, memandu simulator kerumunan melalui representasi berbasis gambar khusus. Dengan cara ini, pengguna dapat dengan mudah dan interaktif memanfaatkan profil perilaku yang diprediksi untuk membuat dan mengendalikan simulasi kerumunan yang sepenuhnya dapat disesuaikan di lingkungan baru sesuai keinginan mereka. Kami melakukan representasi input dan analisis ruang laten MPACT, untuk menunjukkan kemampuan abstraksi dan pembuatan profil metode kami (Bagian 4.2 dan 4.3 ), terlepas dari persyaratan modCCP. Kami mengevaluasi metode kami secara kuantitatif dan kualitatif di Bagian 4.1 dan 4.4 , membandingkan MPACT dengan data nyata dan model dasar melalui pengukuran numerik dan studi pengguna.
2 Pekerjaan Terkait
Simulasi kerumunan dapat didekati dari berbagai tingkatan, masing-masing dengan tujuan yang berbeda. Pada tingkat makroskopis , simulasi berfokus pada pergerakan kerumunan kolektif, mengabaikan detail halus dan navigasi lokal [ JXM*10 , GNL14 , PvdBC*11 , BSK16 ]. Di sisi lain, pada tingkat mikroskopis fokusnya adalah pada navigasi lokal dan detail perilaku tingkat rendah [ R*99 , PAB07 , KSNG17 , vdBSGM11 ]. Pandangan tingkat mesoskopis untuk simulasi memperlakukan agen sebagai entitas individu namun mengkarakterisasi pergerakan mereka melalui hubungan agregat. Metode simulasi dalam kategori ini terutama berfokus pada dinamika kelompok dan bagaimana hal ini memengaruhi navigasi lokal agen [ KO12 , HPNM16 , RCB*17 ], sementara yang lain menggabungkan faktor sosial dan fisiologis [ DGAB16 , XLL*19 ]. Kerumunan yang dapat dipercaya perlu menunjukkan keberagaman baik pada tingkat individu maupun kelompok, sehingga metode mesoskopis kami cocok dalam kasus ini.
2.1 Metode berbasis data dan pembelajaran
Para peneliti telah mengeksplorasi metode berbasis data dan pembelajaran untuk meningkatkan kemungkinan simulasi kerumunan. Metode awal yang murni berbasis data sebagian besar berbasis grafik dan digunakan untuk mencapai perilaku berkelompok dan navigasi [ LCF05 , KLLT08 , YMPT09 ], tanpa secara khusus membahas perilaku yang berbeda. Charalambous dan Chrysanthou [ CC14 ] memperluas konsep ini dengan mengodekan status agen menggunakan representasi temporal, membangun grafik persepsi-tindakan.
Lebih jauh lagi, para peneliti mencoba untuk mereplikasi dinamika kerumunan yang diamati di kerumunan nyata melalui membiarkan agen belajar menggunakan serangkaian contoh [ LCHL07 , LCL07 , LCSCO10 , ZCT18 , XWZ*23 ]. Kerumunan yang dapat diubah oleh Ju et al. [ JCP*10 ] menggunakan lintasan yang diekstraksi dari video dengan model formasi dan lintasan untuk memadukan data masukan dan mensintesis kerumunan dengan perilaku yang diinterpolasi. Tidak seperti pendekatan mereka, kami tidak memanipulasi lintasan nyata tetapi menghasilkan parameter yang memandu jalur simulasi untuk mengungkap perilaku masukan. Kerangka kerja kami juga mendukung data di alam liar tanpa memerlukan anotasi perilaku. Demikian pula, Lee et al. [ LCHL07 ] mempelajari model agen dari lintasan yang diekstraksi dari video untuk menghasilkan tindakan agen berdasarkan gerakan di sekitar, menghasilkan kerumunan yang serbaguna. Sementara sistem mereka sangat mumpuni, metode kami berbeda karena setiap profil kerumunan yang dihasilkan mengintegrasikan beberapa perilaku rumit. Meskipun metode ini dapat menghasilkan berbagai perilaku, efektivitasnya sangat bergantung pada kualitas dan keragaman data, sementara pengendaliannya minimal. Crowd Patches [ YMPT09 ] membangun lingkungan virtual dengan menghubungkan blok yang mengodekan gerakan periodik untuk populasi kecil, menawarkan kontrol dan skalabilitas tetapi tidak memiliki peristiwa dinamis, interaktivitas waktu nyata, dan variasi jalur otomatis—fitur yang ditangani metode kami secara otomatis.
Studi terbaru telah mulai mengeksplorasi teknik deep learning (DL) untuk simulasi kerumunan. Zhang et al. [ ZYJL22 ] mengusulkan kerangka kerja untuk simulasi kerumunan yang secara bersama-sama memungkinkan metode berbasis fisika dan DL untuk saling belajar. Selain itu, teknik reinforcement learning (RL) telah dieksplorasi [ KKPC23 ]. Peng et al. [ PKM*18 ] menggunakan pembelajaran imitasi untuk memandu sistem RL sehingga dapat mengikuti contoh dari video. Namun, pendekatan ini dibatasi oleh data input dan karenanya gagal menunjukkan generalisasi. Hu et al. [ HHB*21 ] memperkenalkan metode RL multi-agen yang mengembangkan kebijakan parametrik, sementara Talukdar et al. [ TZW24 ] menggabungkan RL dengan optimasi Bayesian untuk menavigasi agen di lingkungan yang dinamis. Namun demikian, karya-karya ini berfokus terutama pada penghindaran dan pengarahan tabrakan prediktif, mengabaikan perilaku statis dan interaksi yang lebih halus. Panayiotou et al. [ PKL*22 , PAC25 ] mengusulkan pendekatan berbasis RL untuk mempelajari beragam perilaku kerumunan, termasuk kerangka kerja profil kerumunan yang dapat dikonfigurasi (CCP) yang mempelajari beberapa perilaku secara bersamaan, dan CEDRL, sebuah metode yang mempelajari satu kebijakan atas beberapa set data dunia nyata untuk menangkap berbagai dinamika kerumunan. Charalambous et al. [ CPV*23 ] membahas generalisasi dengan menggunakan deteksi kebaruan pada data lintasan untuk menentukan imbalan imitasi untuk pelatihan agen RL. Sementara itu mempromosikan keragaman dan perilaku baru, itu tidak memiliki pengendalian dan mengabaikan struktur lingkungan. Sebaliknya, model mesoskopik berbasis data kami mengoptimalkan ruang parameter yang ditentukan berdasarkan sinyal kontrol masukan.
2.2 Optimasi parameter
Mayoritas karya tentang mengoptimalkan parameter kerumunan menggunakan data merancang metode untuk menganalisis data sedemikian rupa sehingga hasil analisis memiliki struktur yang kompatibel dengan parameter yang akan dioptimalkan. Sering kali, parameter navigasi dan penghindaran dipelajari misalnya, waktu hingga tabrakan, karena karya awal difokuskan pada parameter simulator umum [ PPD07 , POO*09 , VBJK09 ]. Karya Wolinski et al. [ WJGO*14 ] mampu mengoptimalkan parameter simulasi untuk memenuhi kriteria navigasi kerumunan tertentu. Sementara karya mereka berfokus pada skenario skala kecil hingga menengah, karya tersebut dapat diterapkan pada simulasi skala yang lebih besar dengan mengoptimalkan parameter simulator agar sesuai dengan fitur makroskopis dari diagram fundamental tertentu. Selain itu, Crowd Space [ KSHG18 ] mendefinisikan ruang berdimensi rendah yang menggunakan metrik entropi untuk mengoptimalkan pemilihan algoritma navigasi yang berbeda. Namun, kepadatan rendah dan keragaman data masukan memengaruhi efisiensinya. Demikian pula, Berseth et al. [ BKHF16 ] menerapkan kerangka kerja untuk eksperimen skala besar guna mengkalibrasi parameter algoritma yang menampilkan berbagai tujuan, seperti meminimalkan turbulensi pada titik kemacetan. Namun, pendekatan ini tidak memastikan agen berperilaku dengan benar pada tingkat mikroskopis, terutama berfokus pada pengarahan sambil mengabaikan sifat pengambilan keputusan tingkat tinggi. Pendekatan ini juga beroperasi terutama dalam lingkungan skala kecil. Sebaliknya, MPACT menetapkan profil agen yang dinamis dan terkendali yang berevolusi secara temporal dan spasial, memungkinkan simulasi seperti nyata dengan perilaku interaktif bergerak dan statis, serta dinamika pengelompokan.
2.3 Penulisan dan kontrol
Memiliki alat pembuat yang mudah diakses dan intuitif adalah kunci untuk kerangka kerja yang sukses. Umumnya, ini melibatkan kontrol pengguna atas proses simulasi, atau penyempurnaan hasil yang dihasilkan melalui beberapa jenis UI misalnya, antarmuka Microsoft Office untuk mengendalikan tanggung jawab agen [ All10 ]; survei oleh Lemonari et al. [ LBC*22 ] memberikan tinjauan yang lebih komprehensif tentang masalah ini. Bergantung pada sifat parameter simulasi, proses pembuat dapat memengaruhi komponen simulasi yang berbeda, seperti perilaku tingkat tinggi [ DPA*09 , RPP21 ], perencanaan jalur [ MM17 ] dan pergerakan lokal [ DMCN*17 ]. Dalam karya sebelumnya, perilaku kerumunan dikontrol menggunakan gerakan deformasi untuk formasi dan aliran [ JPCC14 ], manipulasi bobot untuk pengelompokan [ RCB*17 ], bahasa sketsa khusus [ MBA22 ] dan alat yang mudah digunakan seperti kuas, papan cerita, dan bilah geser [ UCT04 , KFS*16 , PKL*22 ]. Interaction Fields oleh Colas et al. [ CvTH*20 ] menyediakan antarmuka penulisan intuitif tempat pengguna dapat menggambar kurva, mendefinisikan pola navigasi lokal, yang berpusat di sekitar titik sumber, menciptakan “bidang interaksi” yang menggambarkan perilaku massa agen. Namun, pengguna perlu membiasakan diri dengan sistem melalui coba-coba, menyiapkan simulasi dari awal. Sebaliknya, antarmuka kami menyajikan perilaku yang disarankan kepada pengguna yang didorong oleh perilaku nyata yang diamati dalam video. Akibatnya, pengguna hanya perlu menyempurnakan hasil sesuai keinginan mereka, menggunakan fungsi intuitif seperti tombol augmentasi lingkungan dan manipulasi slider untuk bobot perilaku dominan.
2.4 Analisis kerumunan
Bahasa Indonesia: Di luar simulasi dan pengendalian kerumunan virtual, memahami dinamika kerumunan dan korelasinya dengan simulasi yang dihasilkan juga penting. Para peneliti telah mengusulkan berbagai metode analisis, dari perbandingan tingkat lintasan hingga wawasan perilaku tingkat tinggi. Guy et al. [ GVDBL*12 ] memperkenalkan metrik statistik berbasis entropi untuk membandingkan set lintasan, menyelaraskan simulasi dengan data nyata untuk mengukur kesalahan residual. Charalambous et al. [ CKGC14 ] mengusulkan pendekatan analisis kedalaman Pareto untuk deteksi outlier untuk mengidentifikasi lintasan anomali dan perilaku lokal di bawah beberapa kriteria yang saling bertentangan. Untuk simulasi skala besar, Wang et al. [ WOO16 ] menerapkan pengelompokan jalur untuk mengekstraksi Pola Jalur laten, sementara kemudian He et al. [ HXZW20 ] menggabungkan fitur bentuk, kecepatan, dan waktu. Amirian et al. [ AZC*21 ] mengkompilasi sebagian besar set data kerumunan dunia nyata dan menganalisis properti statistiknya. Namun, dengan fokus pada perilaku tingkat tinggi, sebagian besar karya bertujuan untuk mengelompokkan pola kerumunan yang “mirip”. Meskipun pendekatan ini mengidentifikasi kemiripan, pendekatan ini sering kali gagal menentukan sifat atau konteks spesifik dari skenario tertentu. Sebaliknya, MPACT dapat diterapkan untuk menyimpulkan dan menggambarkan pola perilaku tingkat tinggi dalam kumpulan data tertentu, termasuk distribusi spasialnya dan bagaimana pola tersebut berkembang seiring waktu.
Dengan membingkai karya kami dalam literatur, kami menggambarkan pendekatan kami sebagai mesoskopik karena kami berfokus pada keadaan suatu area, bukan agen individu. Berbeda dengan karya asli (CCP), dalam kerangka kerja kami, pengguna hanya perlu memberikan lintasan masukan, menyajikan skenario kerumunan yang diinginkan, lalu bobot perilaku spesifik diprediksi secara langsung. Penekanan kami terletak pada aspirasi untuk memfasilitasi simulasi baru dalam lingkungan yang disesuaikan, menggabungkan gerakan kerumunan baru yang terinspirasi oleh dinamika dunia nyata, bukan hanya mereplikasi perilaku yang terekam dalam video.
3 Jalur Pipa MPACT
Bagian ini memberikan perincian alur kerja MPACT: pengaturan pelatihan (Gambar 3 ), dan aplikasi inferensi (Gambar 2 ). Lebih khusus lagi, kami membahas (a) cara kami menghasilkan data pelatihan sintetis menggunakan modCCP—simulator dasar kami, (b) cara kami merepresentasikan data kerumunan dalam ruang gambar dan memperoleh pasangan profil gambar, (c) kerangka kerja pembelajaran, dan (d) cara model digunakan untuk melayani kerangka kerja MPACT, termasuk alat pembuat yang diusulkan.

3.1 Pembuatan data kerumunan sintetis
Menyesuaikan simulator . Seperti yang disebutkan dalam Bagian 1 , kami memodifikasi model kerumunan berbasis RL CCP [ PKL*22 ], dan menggunakan ‘modCCP’ ini sebagai simulator kerumunan yang mendasarinya. Sebelum menjelaskan aspek teknis inti dari simulator yang dimodifikasi, penting untuk menyebutkan bahwa CCP secara inheren berfungsi sebagai kebijakan/jaringan per agen. Pada setiap langkah keputusan, ia mengambil sebagai masukan: (a) profil (satu set bobot perilaku), (b) posisi tujuan dalam ruang 2D dan (c) status agen saat ini. Dengan menggunakan masukan ini, ia menentukan tindakan yang tepat untuk mengarahkan pergerakan agen. CCP terdiri dari pencarian tujuanmathematical equation, pengelompokanmathematical equationInteraksi POImathematical equationdan penghindaran tabrakanmathematical equationbobot, untuk menangkap efek dari memiliki beberapa perilaku dalam simulasi tunggal, dengan mudah, dengan profil yang intuitif dan dapat disesuaikan, yaitu,mathematical equationProfil tidak menyiratkan distribusi tertimbang dari perilakunya di antara agen yang terpengaruh, melainkan semua agen menunjukkan campuran perilaku yang sama.
Meskipun implementasi CCP asli menyediakan sebagian besar fitur yang kami perlukan, kami telah melakukan penyempurnaan untuk menyelaraskannya dengan kebutuhan kami. Pertama, tidak adanya ruang tindakan berkelanjutan dan kebutuhan untuk mengelola penghindaran tabrakan secara manual—melalui bobot khusus—mempengaruhi kualitas pergerakan. Dengan demikian, kami menggabungkan tindakan berkelanjutan dalam kebijakan RL, dan juga mengintegrasikan RVO [ VdBLM08 ] untuk menangani tabrakan secara otomatis, sehingga menghilangkan kebutuhan akan bobot penghindaran tabrakan; detail lebih lanjut di bagian Tindakan di bawah. Pada tahap ini, kami telahmathematical equation-jenis profil, dan untuk lebih meningkatkan pencampuran perilaku, kami menyesuaikan fungsi penghargaan dan memberlakukan batasan yang memastikan total semua bobot perilaku inti selalu sama dengan 1 setiap saat. Terakhir, kami memperkenalkan bobot baru yang disebut ‘konektivitas’mathematical equation, yang mengontrol kedekatan agen, menawarkan spektrum dinamika kelompok yang lebih tinggi; tahap akhir ini menghasilkanmathematical equation-tipe profil. Perhatikan bahwa konsep konektivitas mirip dengan [ RCB*17 ], namun, agen kami menyesuaikan kecepatan masa depan mereka untuk menjaga jarak yang diinginkan dari tetangga mereka, seperti yang didefinisikan olehmathematical equationBagian berikut menguraikan perubahan utama yang telah dilakukan.
Tindakan : kami menangani pergerakan agen dengan menghitung kecepatan masa depanmathematical equationpada setiap langkah pengambilan keputusanmathematical equation, berdasarkan tindakan yang dihasilkan oleh jaringan kebijakan, yang mencakup jarak bergerakmathematical equationdan sudut rotasimathematical equation. Kemudian,mathematical equationditetapkan sebagai kecepatan masa depan yang disukai untuk simulator RVO, yang menyesuaikannya untuk menghindari tabrakan antara agen dan rintangan.
Pengamatan : Selain sensor laser yang ada yang digunakan dalam CCP, kami juga menyertakan pengamatan visual menggunakan sensor grid. Sensor laser memancarkan sinar untuk mendeteksi objek dan mengukur jarak, sementara sensor grid menyediakan pengamatan terstruktur dengan mengodekan hunian objek dalam grid di sekitar agen; kedua sensor disediakan oleh kerangka kerja agen ML Unity [ JBT*20 ]. Modifikasi ini memungkinkan agen untuk mendapatkan ‘rasa’ yang lebih baik tentang keadaan lingkungan, dan merencanakan tindakan masa depan mereka dengan cara yang lebih canggih.
Desain penghargaan : Karena penghindaran tabrakan sekarang ditangani oleh simulator khusus (RVO), kami menghilangkan bobotnya dari kerangka kerja, dengan demikian, untuk setiap langkah simulasimathematical equationtotal hadiahmathematical equationdihitung sebagaimathematical equation, Di mana,
 : bergerak menuju posisi tujuan.
: bergerak menuju posisi tujuan. : berdiri di dekat agen lain, melihat ke arah tengah kelompok,
: berdiri di dekat agen lain, melihat ke arah tengah kelompok, tetangga yang lebih rendah dari ambang batas yang sama dengan 3 m.
tetangga yang lebih rendah dari ambang batas yang sama dengan 3 m. : berdiri di dekat dan melihat ke arah POI,
: berdiri di dekat dan melihat ke arah POI, tetangga yang lebih rendah dari ambang batas yang sama dengan 4m.
tetangga yang lebih rendah dari ambang batas yang sama dengan 4m. : mempertahankan varians kecepatan rendah dan jarak dekat dengan pusat massa gugus agen.
: mempertahankan varians kecepatan rendah dan jarak dekat dengan pusat massa gugus agen. : navigasi lancar, dan penalti hidup.
: navigasi lancar, dan penalti hidup.
Untuk rincian tentang syarat dan ketentuan hadiah individual, lihat Bagian G dari materi tambahan.
Mod pelatihanCCP : Kami secara acak menelurkan 25–40 agen di lingkungan persegi (25mathematical equation25 m) dalam kelompok 1–5, kami mengacak rintangan persegi panjang dan POI dengan ukuran dalam rentangmathematical equation, dan menerapkan strategi berbasis kurikulum seperti yang dijelaskan dalam karya asli [ PKL*22 ].
Menerapkan simulator . Kami melanjutkan dengan memilih bobot perilaku, semua dalam rentang [0,1], mematuhi kendala tambahan bahwamathematical equation. Kami memilih untuk menggunakan keempat bobot parameter ini, seperti yang dijelaskan di atas, karena kami yakin bobot tersebut mampu mencakup berbagai perilaku menengah dan canggih. Perhatikan bahwa bobot konektivitasmathematical equationtidak termasuk dalam batasan ini, berdasarkan rancangan. Ketiga bobot yang disertakan memiliki ketergantungan inheren satu sama lain, misalnya, berinteraksi dengan suatu objek memerlukan penghentian, dan karenanya, dalam kasus tersebut, tidak ada perilaku pencarian tujuan yang kuat. Oleh karena itu, untuk membuat ketergantungan ini lebih jelas bagi pengguna saat menyajikan bobot profil, kami memperkenalkan perhitungan ‘jumlah hingga 1’ ini. Hal ini tidak diperlukan untukmathematical equationkarena perilaku itu sendiri tidak memiliki ketergantungan konseptual dengan yang lain, misalnya, dua orang dapat ‘mencari tujuan’ secara berdekatan, atau terpisah. Untuk profil perilaku tertentu, kami secara acak membuat pengaturan lingkungan (yaitu, rintangan dan POI), menginisialisasi agen, dan membiarkan mereka bergerak hingga 20 detik, cukup untuk menunjukkan perilaku yang ditetapkan, sambil mendokumentasikan lintasan mereka. Simulasi dilakukan dalam 14mathematical equationArea seluas 14 m, berukuran sesuai bagi agen untuk menjalankan perilaku mereka. Di dalam area ini, kami memunculkan 4–10 agen, memastikan mereka dapat menunjukkan perilaku mereka sambil mempertahankan skala yang sebanding dengan data dunia nyata. Dilatih pada rentang ini, model kami paling cocok untuk kerumunan dengan kepadatan yang relatif rendah. Menguji profil prediksi model terhadap kebenaran dasar untuk perilaku yang disintesis dengan jumlah agen yang tidak dilatih (20,30,50,80), mengonfirmasi penurunan yang diharapkan dalam akurasi model, tetapi, meskipun demikian, akurasi prediksi rata-rata dari empat sampel perilaku dengan 20 agen mencapaimathematical equation(proyeksi kehilangan jarak Euclidean terbatas); ini hanya hasil indikatif karena studi komprehensif untuk ini akan melibatkan lebih dari empat sampel dan beberapa iterasi untuk masing-masing sampel. Meskipun demikian, MPACT dapat dilatih ulang pada rentang jumlah agen yang lebih luas, sehingga lebih cocok untuk kerumunan yang lebih padat, jika diperlukan. Kami juga mencatat bahwa, selama pengumpulan data, kami menggunakan area yang lebih kecil daripada dalam fase pelatihan ‘modCCP’ untuk menghindari perubahan profil dinamis. Pada tahap ini kami mengumpulkan sampel yang berisi pasangan (lintasan agen, profil perilaku). Akhirnya, kami berpendapat bahwa pengacakan multifase ini memungkinkan sampel sintetis kami untuk menangkap berbagai variasi, meningkatkan generalisasi model dan mencerminkan keragaman yang ditemukan dalam data kerumunan dunia nyata.
3.2 Representasi data
Selanjutnya, kami membuat kumpulan data yang akan digunakan selama pelatihan. Dengan memiliki pasangan (lintasan agen, profil perilaku) dari modCCP, kami bertujuan untuk memperoleh pasangan kebenaran dasar yang menghubungkan representasi data kerumunan (ruang representasi) dengan serangkaian parameter simulator (ruang parameter). Jadi, untuk ruang parameter , kami memilih empat bobot perilaku yang didefinisikan di Bagian 3.1 .
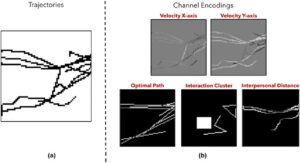
Untuk ruang representasi , kami berpendapat bahwa gambar merupakan pilihan yang tepat untuk mengodekan data kerumunan secara spasial dengan cara yang terstruktur sehingga kami dapat melatih model untuk mengekstrak parameter modCCP. Demikian pula, karena kami bertujuan untuk memprediksi parameter perilaku yang terlokalisasi, kami merasa perlu untuk memasukkan informasi spasial dalam masukan. Pengodean berbasis gambar kami terdiri dari lima saluran, dan masing-masing saluran ini mengodekan properti simulasi tertentu:
1.kecepatan horizontal ,
2.kecepatan vertikal ,
3.jalur paling efisien menuju titik tujuan ( jalur optimal-OP ),
4.cluster interaksi (IC) antara kelompok agen dan sekitar POI,
5.dan terakhir nilai jarak interpersonal (ID) antara kelompok sepanjang simulasi.
Perhatikan bahwa kami tidak menggunakan citra lintasan saja karena tidak memberikan pemahaman lengkap tentang status terkini, dan tidak memiliki detail seperti arah pergerakan; agen yang bergerak dari kiri ke kanan dan dari kanan ke kiri akan memiliki efek visual yang sama. Jadi, kami mengodekan kecepatan sebagai gantinya, yang membantu model memahami komponen navigasi. Saluran yang tersisa dikodekan sebagai berikut. Jalur optimal dibangun dengan menggambar garis lurus yang menghubungkan posisi spawn dan posisi tujuan agen. Kluster interaksi dihasilkan dengan menghubungkan posisi agen, dalam radiusmathematical equation(jarak sosial sebagaimana didefinisikan oleh Hall [ Hal63 ]), yang diam dalam interval waktu yang sama; kami juga menggambar POI di saluran ini (jika ada dalam adegan). Akhirnya, jarak interpersonal memvisualisasikan lintasan pusat massa setiap klaster; agen ditugaskan ke klaster berdasarkan jarak (mathematical equation) dan kesamaan lintasan keseluruhan.
Kami membangun set data pelatihan sintetis dengan memetakan lintasan yang dihasilkan ke ruang gambar melalui pembuatan dan penumpukan lima saluran, sehingga menghasilkan gambar (5,64,64) masing-masing. Gambar 4 menunjukkan contoh penyandian gambar ini dari gambar lintasan referensi (untuk informasi lebih lanjut tentang keacakan dalam penyandian, rujuk materi tambahan Bagian A ). Karena gambar dimaksudkan untuk digunakan sebagai masukan ke model yang dihasilkan, kami mengodekan informasi tambahan melalui intensitas piksel . Pertama, untuk saluran kecepatan, intensitas piksel sesuai dengan kecepatan normalisasi positif atau negatif; kami menetapkan titik tengah intensitas dimathematical equation, dan kami meningkatkan nilai piksel (positif) atau menurunkan (negatif) yang sesuai. Kedua, untuk saluran OP, piksel yang lebih terang menunjukkan deviasi jalur yang lebih rendah dan jarak jalur keseluruhan. Ketiga, untuk saluran IC, nilai piksel yang lebih terang menunjukkan durasi pengelompokan yang lebih lama antara agen. Terakhir, untuk saluran ID, piksel yang lebih terang menyiratkan kedekatan yang lebih dekat antara agen dalam kelompok yang sama. Kami menekankan bahwa gambar yang dihasilkan mengecualikan daerah pemijahan, berkonsentrasi hanya pada gerakan agen dengan hanya menangkap 10mathematical equationBagian tengah lingkungan sepanjang 10 m. Pada tahap ini kami menghasilkan sampel yang berisi pasangan (pengodean gambar, profil perilaku). Kumpulan data sintetis yang dihasilkan terdiri darimathematical equationsampel, dimanamathematical equation, Danmathematical equationdigunakan untuk pelatihan dan validasi.
Studi ablasi pada saluran input telah dilakukan untuk menilai kontribusi pengkodean, mendokumentasikan kinerja model pada Tabel 1 , tujuan dari studi ini adalah untuk memberikan kejelasan dan pembenaran mengenai pilihan pengkodean sebagai representasi data kami. Perhatikan bahwa kami tidak mengablasi saluran kecepatan karena kami menganggapnya penting untuk representasi lintasan. Kami melakukan eksperimen dengan kumpulan data yang lebih kecilmathematical equationsampel, sambil menjaga hiperparameter tetap konstan sepanjang percobaan untuk perbandingan yang adil yaitu, 150 epoch, ukuran batch 256, dan tingkat pembelajaranmathematical equation; rincian pelatihan lebih lanjut dibahas kemudian di Bagian 3.3 .
Kerugian  |
Akurasi  |
|||||
|---|---|---|---|---|---|---|
| Saluran | Kereta | Val. |  |
 |
 |
 |
| Semua (5) | 1.019 | 1.613 | 0.786 | 0,669 tahun | 0.733 | 0.763 |
| tanpa OP | 1.031 | 1.620 | 0.756 | 0.642 | 0.733 | 0.762 |
| tanpa IC | 1.150 | 1.708 | 0.731 | 0,559 | 0,568 tahun | 0,749 tahun |
| tanpa identitas | 1.018 | 1.602 | 0,797 tahun | 0.682 | 0.747 | 0,755 tahun |
| hanya OP | 1.160 | 1.703 | 0,735 | 0.543 | 0.553 | 0.612 |
| hanya IC | 1.035 | 1.617 | 0,767 tahun | 0.661 | 0.726 | 0.737 |
Teks tebal menunjukkan nilai terbaik untuk setiap kolom.
Berdasarkan temuan Tabel 1 , kita dapat menyimpulkan bahwa yang paling tidak signifikan adalah kanal ID karena dengan menghilangkannya akan menghasilkan kerugian paling rendah dan akurasi paling tinggi, kecuali tentu saja akurasi nilai konektivitas. Namun, terlihat bahwa perbedaannya dengan model ‘input penuh’ hampir tidak berarti, dan demimathematical equation, kami memilih untuk melanjutkan dengan memanfaatkan kelima penyandian sebagai saluran masukan untuk model kami. Dari tiga saluran yang dihapus, Tabel 1 mengungkapkan IC sebagai yang paling penting, yang masuk akal mengingat ia menyediakan informasi baik untuk pengelompokan dan interaksi dengan POI. Untuk visualisasi penyandian lebih lanjut, Gambar 5 mengilustrasikan contoh lintasan dan penyandian untuk perilaku dominan per bobot yaitu, profil dominan tujuan, dominan kelompok, dan dominan interaksi. Contoh-contoh ini mengonfirmasi intuisi kami bahwa saluran OP berguna dalam menilai seberapa menonjol bobot tujuan, sedangkan saluran IC memberikan informasi berharga mengenai dampak bobot kelompok dan interaksi.

3.3 Pelatihan model MPACT
Setelah membangun kumpulan data sintetis, kami melanjutkan untuk melatih model MPACT untuk mengambil sebagai masukan penyandian gambar (diperkenalkan di Bagian 3.2 ) dan mengeluarkan profil perilaku mendasar yang cocok dengan tugas kerumunan yang diamati dalam gambar. Tujuan kami adalah untuk menemukan pemetaan antara ruang gambar dan ruang parameter kerumunan sehingga memungkinkan untuk mengamati perilaku di alam liar dan memparameterisasinya dengan cara yang: dapat dipahami (bobot perilaku intuitif), dapat disesuaikan (intervensi pengguna yang mudah), dan dapat digunakan sebagai blok penyusun untuk simulasi khusus yang baru (melalui UI).
Selama pelatihan, kami lebih jauh menambah data kami dengan menerapkan operasi transformasi secara acak ke gambar, yaitu rotasi dan pembalikan. Secara khusus, kami tidak mengizinkan rotasi acak penuh karena hal ini dapat menyebabkan hilangnya informasi, misalnya, rotasimathematical equationpada gambar dengan nilai pada piksel sudutnya, akan mengakibatkan hilangnya informasi. Jadi, kami mendefinisikan empat rentang [80mathematical equation, 100mathematical equation], [170mathematical equation, 190mathematical equation], [260mathematical equation, 280mathematical equation], [350mathematical equation, 370mathematical equation] yang dapat dipilih sudut acaknya. Seperti yang disebutkan sebelumnya, input model kami adalah lima saluran 64mathematical equation64 gambar dan keluaran akhir sesuai dengan empat nilai bobot perilaku. Model ini memiliki tiga lapisan konvolusional (ukuran kernel = 3, dropout = 0,2), diikuti oleh empat lapisan yang terhubung penuh (dropout = 0,5). Keluaran dari lapisan linier terakhir adalah vektor bernilai enam. Gambaran singkat dari pengaturan masukan/keluaran model kami ditunjukkan pada Gambar 6 .
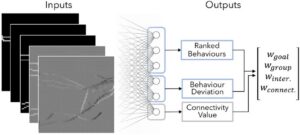
Berdasarkan rancangannya, model tersebut tidak secara langsung meregresikan keempat bobot perilaku. Tiga nilai pertama dari output digunakan untuk memberi peringkat perilaku dominan, yang dilatih dengan kerugian entropi silang. Pada dasarnya, nilai-nilai tersebut mewakili keyakinan bahwa setiap perilaku inti adalah yang paling dominan. Dua nilai berikutnya (mathematical equation) dirancang untuk mewakili perbedaan perilaku paling dominan, kedua dan ketiga yang paling dominan, yaitu,mathematical equation, Danmathematical equationDari perbedaan yang dihasilkan, bobot yang diprediksimathematical equationdapat dihitung menurut Persamaan ( 1 ), dan dilatih dengan kehilangan L1. Kami mendekati masalah menggunakan pembelajaran multi-tugas (MTL), di mana satu tugas adalah untuk memprediksi perilaku dominan, dan yang lainnya untuk memperkirakan hubungan numerik di antara keduanya. Demikian pula, beberapa karya menerapkan MTL untuk tugas yang berbeda, seperti kombinasi klasifikasi dan regresi [ CRH*24 , KJBS24 ], atau pemeringkatan dan regresi [ ZY10 ]. Desain model ini, berkinerja lebih baik dan membutuhkan lebih sedikit data pelatihan. Kami berasumsi bahwa kinerja yang lebih tinggi disebabkan oleh ruang prediksi yang terbatas; dengan terlebih dahulu memiliki pemeringkatan, model diberi konteks lebih lanjut dan dengan demikian membatasi jenis kombinasi untuk diprediksi.

Terakhir, output akhir diatur agar sesuai dengan nilai konektivitasmathematical equation, dan juga dilatih dengan kehilangan L1; kami mengisolasi konektivitas karena dapat hidup berdampingan dengan semua perilaku lain dan lebih berfungsi sebagai pengubah jarak daripada perilaku inti. Oleh karena itu, fungsi kerugian akhir kami diberikan oleh:
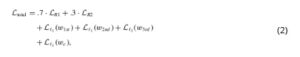
Di manamathematical equationBahasa Indonesia:mathematical equationadalah kerugian entropi silang dari perilaku yang paling dominan dan paling dominan kedua, secara berurutan. Kami memprioritaskan bobot regresi (kerugian L1) dengan memberikannya kepentingan yang lebih tinggi karena bobot tersebut sesuai dengan keluaran akhir kami, sementara kami menyeimbangkan kerugian dari perilaku yang paling dominan pertama (0,7) dan kedua (0,3), karena yang dominan adalah yang memiliki dampak terbesar pada perpaduan perilaku yang dihasilkan. Kami mencatat bahwa nilai penyeimbangan tertentu telah dipilih melalui coba-coba.
Setelah model dilatih, kami menggunakan set validasi dan ambang batas toleransimathematical equationuntuk menghitung akurasi individual. Kami memilih toleransi ini karena kami mengamati bahwa perbedaan yang lebih kecil dalam nilai bobot tidak memiliki dampak yang nyata pada perilaku yang dihasilkan. Model kami mampu memprediksi perilaku yang paling dominan dan paling dominan ke-2 dengan akurasi masing-masing 87% dan 74%. Lebih jauh, mengenai perilaku individual, model memprediksi bobot pencarian tujuan, pengelompokan, interaksi, dan konektivitas dengan akurasi masing-masing 79%, 68%, 75%, dan 77%.
Studi ablasi tambahan telah dilakukan untuk menekankan perlunya empat perilaku yang disebutkan di atas (Tabel 2 ). Kami memperbaiki nilai hiperparameter dan melatih model yang lebih kecil, mendokumentasikan perbedaan antara jarak yang ditempuhmathematical equationoleh agen yang mengikuti model kami dan kebenaranmathematical equationoleh agen kebenaran dasar. Kami menghitung jarak yang ditempuh sebagaimathematical equation, membandingkan setiap agen nyata dengan agen simulasi yang sesuai. Kami menggunakan tiga cuplikan data dunia nyata dari jalan yang ramai, kampus universitas, dan halaman gereja (Zara, Students, and Church [ LCL07 , CC14 ]). Memeriksa keragaman perilaku secara kuantitatif merupakan tantangan, oleh karena itu, kami memerlukan metrik yang sederhana namun ekspresif untuk digunakan dalam studi ini. Pilihan kami untuk menggunakan metrik ‘jarak yang ditempuh’ berasal dari kebutuhan akan metrik representatif yang menunjukkan kesetiaan perilaku karena kami mempelajari kegunaan perilaku individu. Misalnya, jika kami menggunakan kepadatan, maka pengelompokan tiga versus sepuluh orang akan dianggap salah meskipun perilaku yang mendasarinya sama. Tabel 2 menunjukkan kebutuhan perilaku yang kami pilih karena, secara rata-rata, model lengkap berkinerja terbaik. Hasil per set data juga masuk akal karena set data Zara sebagian besar terdiri dari orang-orang yang berjalan menuju tujuan mereka, sehingga menghilangkan perilaku tujuan paling merusak kinerja. Dengan cara yang sama, set data Gereja tidak mengandung perilaku interaksi apa pun, oleh karena itu menghilangkan bobot interaksi sebenarnya bermanfaat bagi kinerja. Dengan mempertimbangkan keberagaman perilaku dunia nyata, kami mendasarkan pilihan kami untuk menggunakan keempat perilaku tersebut pada metrik rata-rata dari tiga klip data.
| Kumpulan data | Zara | Siswa | Gereja | Rata-rata |
|---|---|---|---|---|
| Model | Jarak yang ditempuh berbeda (m)  |
|||
| Model Lengkap | 2.908 | 4.972 | 3.258 | 3.713 |
| tanpa Tujuan | 10.173 | 6.555 | 10.728 | 9.152 |
| tanpa Grup | 4.267 | 7.773 | 8.096 | 6.712 |
| tanpa Inter. | 4.175 | 6.043 | 2.711 | 4.310 |
| Koneksi Tetap. | 2.888 | 5.761 | 5.196 | 4.615 |
Teks tebal menunjukkan nilai terbaik untuk setiap kolom.
3.4 Memanfaatkan model yang terlatih
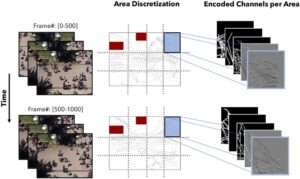
Pada tahap ini, kami memiliki model MPACT terlatih yang siap diaplikasikan pada data yang tak terlihat dari lintasan nyata yang diekstraksi dari video. Setiap skenario didiskritisasi baik dalam waktu maupun ruang. Untuk ini, kami menggunakan jendela waktu yang tepat untuk setiap kumpulan data (yaitu, 125, 250 atau 500 bingkai video), dan menurut rasio aspek video (4:3 dalam kasus kami) kami membagi ruang menjadi area yang lebih kecil yang masing-masing akan memiliki profil perilaku mereka sendiri, seperti yang diisyaratkan pada Gambar 7. Pada tahap ini kami bertujuan untuk memprediksi profil setiap area, untuk setiap jendela waktu, hanya dengan lintasan yang diekstraksi. Di sini, kami ingatkan bahwa sampel pelatihan sintetis mengodekan simulasi yang dilakukan dalam 10mathematical equationLingkungan 10 m, jadi kami mendiskritisasi untuk membawa data uji lebih dekat ke data pelatihan. Dengan video uji kami, kami menemukan yang terbaik untuk membaginya dalam 12 bagian tersebut. Tentu saja, ini tidak universal di semua data yang mungkin, memotivasi penelitian lebih lanjut tentang bagaimana diskritisasi ini harus terjadi. Kami mencatat bahwa untuk setiap set data, kami membangun peta lingkungan dengan memposisikan rintangan dan POI seperti yang ditentukan. Mengingat diskritisasi ruang dan waktu, lintasan agen diekstraksi secara khusus untuk setiap area perilaku dan untuk setiap kerangka waktu, untuk membuat set gambar input (untuk eksperimen dengan prediksi jendela bergeser, lihat materi tambahan Bagian B ). Kami mencatat bahwa, mengingat dimensi dunia nyata (dalam meter) dari lingkungan, kami dapat mendeteksi bagaimana setiap area perilaku meluas dan mengumpulkan lintasannya. Kemudian, set gambar untuk setiap area dimasukkan ke dalam model terlatih yang menghasilkan serangkaian profil yang diprediksi per area.
Sebagai komponen terakhir dalam alur kerja kami, kami mengizinkan intervensi pengguna melalui antarmuka penulisan yang memfasilitasi (a) mensintesis kerumunan baru yang berperilaku sesuai dengan perilaku masukan, dan (b) penyesuaian manual bobot parameter. Dengan kumpulan data kerumunan, model kami mengekstrak profil perilaku spasio-temporal yang dapat langsung digunakan untuk merekonstruksi tugas kerumunan tingkat tinggi yang diamati dalam data masukan, atau disesuaikan dan didistribusikan secara strategis dalam lingkungan untuk menghasilkan skenario kerumunan baru dengan konteks yang serupa. Gambar 8 menunjukkan ikhtisar alat penulisan kami, yang mengisyaratkan fungsinya: (a) pengguna membuat lingkungan khusus dengan membuat tata letak area, mengatur posisi dan skala rintangan/POI, dan posisi spawn/goal agen, (b) kemudian algoritma pengelompokan menyajikan kepada pengguna perilaku yang disarankan, seperti yang diprediksi oleh model kami dan akhirnya (c) pengguna menetapkannya ke area lingkungan tertentu untuk jangka waktu tertentu. Demonstrasi setiap fitur UI disediakan dalam materi video tambahan yang menyertainya.
Selain itu, kami menggunakan algoritma pengelompokan DBSCAN [ EKS*96 ], dengan parameter epsilon = 0,125, minSamples = 1 , untuk mengelompokkan bersama profil perilaku yang diprediksi serupa dan menunjukkan kepada pengguna pusat klaster sebagai profil yang dominan perilaku (prefab) untuk lebih memudahkan penulisan. Selain itu, pengguna dapat memodifikasi perilaku yang direplikasi sesuai dengan preferensi mereka, karena kami memungkinkan mereka untuk memilih area tertentu—memilih kerangka waktu dan lokasi grid yang disukai—dan menyesuaikan nilai parameter yang diprediksi menggunakan bilah geser yang mudah digunakan. Kami mengurangi kebutuhan untuk secara manual menentukan nilai parameter dari awal, yang berarti bahwa pengguna seharusnya dapat menemukan hubungan antara perilaku yang diamati dan parameter masing-masing melalui coba-coba.
4 Hasil
Model kami telah dilatih pada komputer pribadi, menggunakan CPU 12-core, RAM 64GB, dan GPU NVIDIA RTX 2070 (8GB). Pelatihan memakan waktu sekitar 9,5 jam untuk 500 epoch, menggunakan ukuran batch dan kecepatan pembelajaran yang sama dengan 256 danmathematical equation, masing-masing. Untuk optimasi, kami menggunakan algoritma AdamW dan mengatur peluruhan bobot sama denganmathematical equationSebelum menyajikan analisis, hasil, dan evaluasi utama kami, kami melakukan uji konsistensi diri untuk memastikan bahwa MPACT memang dapat mengenali perilaku dominan (untuk analisis ini, rujuk materi tambahan Bagian C ).
Awalnya, kami menilai metode kami secara kuantitatif dengan mengukur kinerjanya terhadap data dunia nyata, pekerjaan dasar terpilih, dan simulator berbasis data terkini (GREIL, CEDRL [ CPV*23 , PAC25 ]). Untuk perbandingan kuantitatif dasar , kami memilih kerangka kerja RVO, CCP ‘dasar’, dan Random Walk yang ada [ VdBLM08 , PKL*22 , GAK62 ]. Untuk Random Walk, setiap agen menavigasi dengan menetapkan arah pergerakan acak (-45mathematical equationBahasa Indonesia: , 0mathematical equationatau 45mathematical equation), dengan frekuensi yang sama seperti ‘modCCP’ memilih tindakan baru. Kami menggunakan parameter RVO yang identik seperti yang digunakan dalam model parameter yang mendasarinya (Bagian 3.1 ), dan ‘dasar’ CCP mengacu pada pemilihan bobot CCP yang paling sesuai dengan video berdasarkan observasi empiris dan penilaian kualitatif; kami mencantumkan nilai-nilai ini di Bagian 4.1 . Berikutnya, kami menilai representasi input kami (pengodean gambar lima saluran) dan kemampuannya untuk merepresentasikan data kerumunan dengan cara yang terstandarisasi (lihat Bagian 4.2 ). Kemudian, di Bagian 4.3 , kami mengeksplorasi kapabilitas ruang laten MPACT dan sejauh mana ia menyediakan pemetaan ke ruang parameter yang dapat dijelaskan dan digunakan. Akhirnya, untuk evaluasi kualitatif , kami melakukan dua studi pengguna terpisah (Bagian 4.4 ) yang secara inheren membandingkan MPACT dengan data riil, RVO, dan bobot CCP yang ditentukan secara manual; cuplikan hasil animasi dapat ditemukan di video tambahan .
Untuk percobaan kami, kami menggunakan tiga set data: Students, Zara, dan Church (seperti yang diperkenalkan di Bagian 3.3 ). Untuk setiap video, kami menggunakan lintasan agen nyata untuk membangun penyandian berbasis gambar yang sesuai, yang masing-masing mewakili area dan rentang bingkai tertentu.
4.1 Evaluasi kuantitatif
4.1.1 Pengujian pada data dunia nyata
Kami menerapkan model kami lagi pada tiga set data dunia nyata untuk mendapatkan parameter kerumunan (profil perilaku) setiap area pada setiap jendela waktu. Kemudian, kami menggunakan parameter ini dan menjalankan simulasi dengan tetap mempertahankan posisi spawn/tujuan agen asli, mendokumentasikan lintasan yang dihasilkan. Untuk menilai kerangka kerja kami secara kuantitatif, kami menggunakan empat metrik: kepadatan, kecepatan [ Wei93 , Fru71 ], jarak ke tetangga terdekat (DNN) [ HJAA07 ] dan keragaman arah pergerakan (MDD). Kami menghitung kepadatan lokalmathematical equationdari seorang agenmathematical equationpada waktumathematical equationsebagai:
![]()
Untuk DNN kami menggunakan KDTree untuk secara efisien menemukan tetangga terdekat (dalam radius 3,6 m) dari setiap agen di setiap langkah waktumathematical equationdan kumpulkan jarak yang sesuai. Akhirnya, untuk MDD, kita buat vektor gerakanmathematical equationsetiap 4 detik, lalu hitung MDD (daftar nilai) untuk agenmathematical equationmenggunakan:
![]()
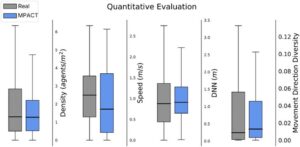
Pada dasarnya, metrik ini digunakan untuk mengukur kesamaan perilaku antara skenario nyata dan simulasi; untuk setiap metrik, kami menggabungkan nilai untuk semua agen, di semua langkah waktu. Terutama, agen dalam video berjalan, berputar, dan berdiri diam. Kombinasi gerakan ini mengungkapkan perilaku mereka, misalnya, jika agen berjalan dan kemudian berhenti untuk jangka waktu yang lama, maka mereka cenderung mengelompokkan atau memeriksa POI di dekatnya. Sebaliknya, jika dua agen bergerak terus-menerus sementara memiliki DNN rendah, mereka mungkin memiliki perilaku dominan tujuan dengan nilai konektivitas yang tinggi. Oleh karena itu, jika dua populasi (nyata dan yang dihasilkan MPACT) memiliki distribusi yang sama dari metrik yang dipilih ini, kami yakin itu adalah ukuran indikatif dari kesamaan perilaku secara keseluruhan. Kami memvisualisasikan distribusi metrik tersebut yang sesuai dengan lintasan nyata dan simulasi pada Gambar 9. Hasilnya menunjukkan bahwa tren keseluruhan dari distribusi nyata kompatibel dengan yang disimulasikan, terutama dalam median dan rentang interkuartil (IQR) [ Moo09 ]. Meski begitu, kemiripan kumis kotak-plot ini sebagian subjektif; kumis tersebut memberikan pandangan global yang disederhanakan dari data, sehingga kita belum dapat mengklaim kesetiaan terhadap perilaku nyata dengan kepastian mutlak.
Selain itu, pada Gambar 10 kami menyediakan korespondensi visual lintasan nyata dan simulasi dengan profil dasar yang dijadikan sampel; MPACT diterapkan pada data dunia nyata untuk memprediksi profil kerumunan yang kemudian digunakan untuk menghasilkan tiga simulasi dengan posisi spawn dan goal yang diacak. Kami menunjukkan bahwa semua run secara kontekstual mirip dengan skenario nyata yang sesuai, dalam hal perilaku kerumunan. Dalam semua kasus, beberapa agen tetap diam sementara yang lain bergerak, terkadang berhenti untuk bertemu dan berinteraksi dengan yang lain.

4.1.2 Perbandingan
Kami melakukan eksperimen lebih lanjut untuk mengevaluasi kualitas kerangka kerja kami dibandingkan dengan ‘garis dasar’ yang ada. Secara khusus, kami menggunakan model berikut, (a) RVO, (b) random walk dan (c) CCP baseline yaitu, memiliki satu profil statis yang ditentukan secara manual di seluruh data. Untuk yang terakhir, kami memperkirakan profil universal {mathematical equation} dengan menganalisis kemunculan setiap perilaku inti dalam tiga set data. Kami menggunakan (b) untuk berfungsi sebagai garis dasar kontrol, (a) untuk berfungsi sebagai metode yang mapan dan digunakan secara luas dan (c) sebagai pemanfaatan langsung dari simulator yang mendasarinya, tanpa pengoptimalan parameter apa pun. Ketiga pilihan tersebut disengaja untuk memberikan beberapa perspektif tentang alternatif yang logis. Pilihan profil yang lebih cermat untuk setiap set data, setiap rentang bingkai, dan setiap area dapat dibuat, yang kami jelajahi lebih lanjut selama studi ‘pakar’ kami di Bagian 4.4.2 . Karena menilai kesamaan distribusi secara visual misalnya, box-plot, agak subjektif, kami juga menghitung divergensi Jensen–Shannon (JSD) [ Lin91 ] antara distribusi setiap jenis metrik sebagaimana dihitung dari lintasan nyata dan lintasan simulasi per model. JSD adalah variasi dari divergensi KL dan dibatasi dalam rentang [0,1] dengan nilai yang lebih dekat ke 0 yang menunjukkan distribusi probabilitas yang serupa. Tabel 3 menyajikan skor JSD antara distribusi per-metrik nyata dan simulasi, saat menggunakan berbagai klip dari semua set data yang tersedia; kami menggunakan total 95 detik. Perhatikan bahwa setiap distribusi per-metrik berisi semua nilai individual untuk semua agen, di semua langkah waktu. MPACT memiliki skor JSD terendah untuk tiga dari empat metrik yang menunjukkan bahwa itu dapat berfungsi sebagai garis dasar baru atau setidaknya sebanding dengan garis dasar CCP dan RVO.
| Metrik | Kepadatan | Kecepatan | TTL | Arah
Keberagaman |
|---|---|---|---|---|
| Model | JSD  |
|||
| MPAK | 0,0167 tahun | 0.173 | 0,0355 | 0,0137 pukul 0,0137 |
| Garis dasar PKT | 0,0189 | 0.315 | 0,0421 pukul 0,0421 | 0,0113 |
| RVO | 0,0171 tahun | 0.483 | 0,0476 tahun | 0,0753 tahun |
| Jalan acak | 0,0651 tahun | 0.461 | 0,0978 pukul | 0.246 |
Teks tebal menunjukkan nilai terbaik untuk setiap kolom.
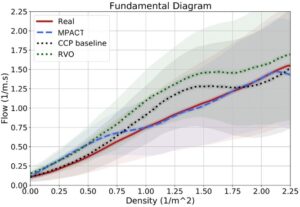
Dengan menyelidiki lebih lanjut, kami membangun diagram fundamental (FD) [ FMN18 , Fru71 ] yang membandingkan tren data dunia nyata dan data simulasi. FD digunakan secara luas dalam domain simulasi kerumunan baik dalam bentuk kecepatan/kepadatan atau aliran/kepadatan. Mereka adalah cara yang kuat untuk memvisualisasikan interaksi karakteristik kerumunan makroskopis utama. Untuk FD pada Gambar 11 , kami menggabungkan kumpulan data Students dan Zara yang menghasilkan total 562 lintasan agen dan simulasi 9,5 menit. Kepadatan lokal setiap agenmathematical equationpada setiap langkah waktumathematical equationdihitung lagi dengan Persamaan ( 3 ), dan semua nilai diagregasi. FD menunjukkan kesamaan yang lebih tinggi antara simulasi dunia nyata dan MPACT, dibandingkan dengan baseline RVO dan CCP. Metode yang terakhir tampaknya menghadapi aliran yang lebih tinggi pada kepadatan sedang.
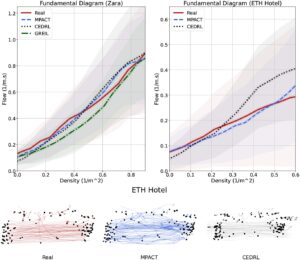
Simulator kerumunan canggih . Sementara MPACT bukan simulator kerumunan khusus, kami juga menilai bagaimana kinerjanya terhadap dua model berbasis data terbaru yang menawarkan keragaman perilaku: GREIL [ CPV*23 ] dan CEDRL [ PAC25 ]. Kami membangun FD menggunakan dua set data dunia nyata dan menyajikan hasilnya pada Gambar 12 . Yang pertama, Zara, digunakan selama pelatihan GREIL dan CEDRL. Simulasi dengan ketiga model—menggunakan waktu spawn, posisi, dan sasaran nyata—menunjukkan bahwa MPACT mengungguli GREIL, dalam skenario ini, dan berkinerja sebanding dengan CEDRL, meskipun dilatih hanya pada data sintetis. Untuk mengevaluasi generalisasi lebih lanjut, kami menggunakan set data ETH Hotel [ PESVG09 ], yang tidak disertakan dalam pelatihan CEDRL maupun MPACT. Dalam pengaturan ini, simulasi yang dihasilkan MPACT lebih selaras dengan statistik dunia nyata, sedangkan CEDRL menunjukkan aliran yang lebih tinggi pada kepadatan yang lebih tinggi; GREIL dikecualikan dari pengaturan ini, karena memerlukan kebijakan terlatih khusus kumpulan data yang tidak tersedia. Selain itu, kami memetakan jalur simulasi yang dihasilkan pada Gambar 12 , di mana intensitas warna yang lebih rendah menunjukkan kecepatan agen yang lebih tinggi. Sejalan dengan hasil FD, agen CEDRL cenderung bergerak lebih cepat dan menunjukkan perilaku yang lebih langsung dan berorientasi pada tujuan, sementara agen MPACT tampaknya lebih baik menangkap perilaku antara yang disajikan dalam data.
Meskipun FD mencerminkan dinamika massa secara keseluruhan, FD mungkin mengabaikan aspek-aspek yang lebih rinci seperti navigasi yang lancar atau interaksi yang terperinci. Namun, FD menunjukkan bahwa pendekatan kami berkinerja secara kompetitif dengan metode-metode terkini, sekaligus menawarkan fitur-fitur penulisan dan pengendalian yang terbatas atau tidak ada dalam model-model yang dibandingkan.
4.2 Analisis representasi
Berikutnya, kami menyelidiki sejauh mana representasi berbasis gambar kami (diformulasikan dalam Bagian 3.2 ) mengabstraksikan data kerumunan ke dalam ruang representasi terstruktur, di mana data dengan perilaku dasar yang serupa berada berdekatan satu sama lain.
Untuk mengukur seberapa ‘dekat’ representasi tersebut, kami menggunakan kerangka kerja pembelajaran kontrastif (pembelajaran kontrastif sederhana dari representasi—SimCLR [ CKNH20 ]) untuk mempelajari ruang laten terstruktur berdasarkan pasangan (pengodean berbasis gambar, profil perilaku). Dengan memvisualisasikan ruang laten yang dipelajari (Gambar 13 -atas), kami mengharapkan representasi terkompresi dari perilaku serupa untuk membentuk kluster misalnya, data pencarian tujuan yang dihasilkan dari RVO dekat dengan data dominan tujuan dari simulator CCP asli, sedangkan data kelompok atau interaksi berbeda. Kami menyajikan vektor laten dari tiga jenis data. Segitiga terbalik menunjukkan pengodean perilaku dominan dari generator yang berbeda (CCP, RVO, modCCP) dan contoh (2 CCP berjalan untuk profil yang sama). Kami juga mengilustrasikan pengodean yang mewakili skenario ‘kompleks’ yang sama (Zara, Church, Students), diambil dari data nyata, pakar, dan modCCP, dan terakhir beberapa data pelatihan dengan perilaku dominan (titik 3 warna). Ruang terstruktur, karena representasi perilaku dominan berada dalam kelompok umum. Sampel dengan perilaku menarik lebih tersebar luas tetapi tetap terstruktur (poin Siswa membentuk kelompok yang lebih kecil) dan didistribusikan menurut tugas kelompok yang paling mirip; kami tidak mengharapkan mereka berkumpul di sekitar kelompok laten yang dominan, jika tidak, skenarionya akan mudah sejak awal, menggantikan kebutuhan akan representasi alternatif. Kami juga tidak mengharapkan pengelompokan yang berbeda, misalnya, semua sampel Siswa bersama-sama, karena data nyata secara alami menghadapi keragaman, dan perilaku (dan dengan demikian pengodean) berubah seiring waktu dan lokasi.
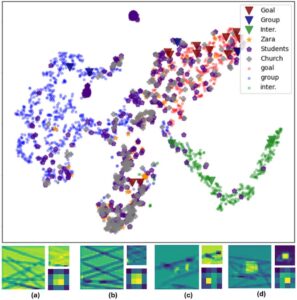
Karena jaringan yang dilatih hanya melihat representasi berbasis gambar, yaitu, tidak memiliki informasi tentang perilaku yang mendorong data, ruang laten terstruktur menyiratkan bahwa representasi berbasis gambar yang kami usulkan berisi fitur yang sesuai, yang mengodekan tugas kerumunan yang mendasarinya, bahkan jika data itu sendiri (lintasan) bervariasi. Sebagai wawasan tambahan, pada Gambar 13 -bawah, kami menyediakan peta fitur (seperti yang diekstraksi dari lapisan konvolusi dalam tiga kedalaman berbeda) dari skenario yang dominan-tujuan, pengelompokan, dan interaksi dengan POI. Kami mengamati bahwa model yang dilatih cenderung fokus pada fitur yang sama ketika representasi mengodekan skenario yang sebanding (misalnya, pencarian tujuan dalam [a] dan [b]), sedangkan perilaku yang berbeda menunjukkan fitur yang berbeda. Oleh karena itu, representasi kami bermakna, efektif, dan dapat digeneralisasikan, yaitu, independen dari generator data yang mendasarinya. Dibandingkan dengan representasi data kerumunan alternatif misalnya, berbasis fitur [ KSHG18 ], pengodean kami kompatibel dengan model (model MPACT), yang memperluas peluang penggunaan umumnya; representasi ini kemudian dapat digunakan untuk membuat kumpulan orang baru melalui antrian kontrol tingkat tinggi yang implisit.
4.3 Analisis ruang laten MPACT
Kami juga menilai sejauh mana model MPACT memetakan data kerumunan (pengodean) ke dalam ruang laten yang digeneralisasi, dapat ditafsirkan, dan dapat dikontrol. Kami memvisualisasikan ruang laten MPACT dalam ruang segitiga 2D. Karena sifat bobot profil, yaitu,mathematical equation, kami memetakan setiap sasaran perilaku inti , pengelompokan , dan interaksi ke dalam titik sudut segitiga. Kemudian kami menggunakan koordinat Barycentric untuk menempatkan setiap sampel di ruang tersebut; konektivitas direpresentasikan oleh ukuran setiap penanda.
Tujuannya adalah untuk mencapai metode yang independen terhadap generator, yang menyediakan wawasan yang dapat dijelaskan mengenai perilaku kerumunan, dan kontrol pengguna tingkat tinggi dengan kemampuan penulisan. Jadi, kami memvisualisasikan profil yang diprediksi MPACT untuk tiga set data dunia nyata (Gambar 14a ), bersama dengan prediksi simulasi modCCP nyata dan profil yang dipilih ‘pakar’ (Gambar 14b ). Untuk yang terakhir, enam pengguna pakar diperlihatkan klip berdurasi 20 detik dari video kerumunan yang berbeda dan diminta untuk meniru perilaku yang mereka amati menggunakan UI kami; replikasi mengacu pada penangkapan perilaku yang serupa dan bukan jalur agen yang tepat. Mereka melakukannya dengan menetapkan profil perilaku (dalam bentukmathematical equation) ke area yang ditentukan untuk setiap jendela 5 detik; setiap pengguna dapat menyempurnakan pilihan mereka sebanyak yang mereka inginkan. Tiga klip yang ditampilkan berasal dari video Church, Zara, dan Students, yang diberikan kepada pengguna dalam urutan ini agar sesuai dengan meningkatnya kompleksitas perilaku. Kami menggunakan posisi spawn dan goal yang sebenarnya dari setiap set data, sehingga memudahkan pengguna untuk membandingkan perilaku yang dihasilkan dengan video. Untuk setiap pengguna dan skenario, kami melacak waktu yang dihabiskan, lintasan yang disimulasikan, dan profil yang dipilih. Namun, untuk analisis bagian ini, kami hanya menggunakan profil yang mereka pilih; analisis lebih lanjut tentang waktu yang dihabiskan dan lintasan yang disimulasikan dapat ditemukan nanti di Bagian 4.4.2 . Kami kemudian:
- Amati distribusi dalam ruang laten (Gambar 14a ), dan struktur spasio-temporal (Gambar 14b ).
- Menyimpulkan bagaimana skenario yang tidak diketahui diklasifikasikan (Gambar 15 ).
- Menyajikan cara memanfaatkan keragaman yang dipelajari untuk secara intuitif menulis khalayak yang dituju (Gambar 16 ).
Setiap titik yang divisualisasikan mewakili area tertentu pada jangka waktu tertentu dari masing-masing skenario, misalnya, 20 detik pertama dari kisi kiri atas data Zara. Gambar 14a menunjukkan bahwa skenario Zara sebagian besar digerakkan oleh tujuan, sementara Siswa menunjukkan pengelompokan yang lebih kuat. Umumnya, interaksi dengan POI tidak sering ditemukan dalam skenario inferensi ini. Temuan ini mengungkapkan bahwa ruang laten MPACT memberikan wawasan tentang jenis kerumunan ( dapat dijelaskan ) yang terdiri dari data input melalui pengamatan distribusi perilaku.
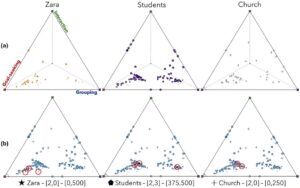
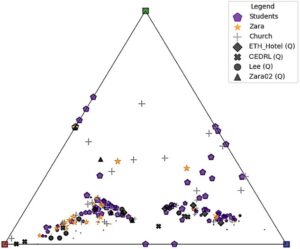

Untuk memverifikasi bahwa ruang MPACT bermakna dan terstruktur, pertama-tama kami memetakan contoh-contoh dari serangkaian titik yang sesuai dengan skenario yang sama (lokasi grid tetap dan kerangka waktu) yang bersumber dari metode pembangkitan yang berbeda, yaitu, tangkapan nyata, modCCP, dan pakar (Gambar 14b ); karena kami memiliki 6 pakar, kami merata-ratakan titik-titik pakar yang serupa untuk pengamatan yang lebih adil. Kami mengonfirmasi bahwa titik-titik ini berada dalam area laten yang sama dengan sedikit deviasi yang dapat dikaitkan dengan bias generator misalnya, pengenalan pakar dengan berbagai skenario kerumunan dan area simulasinya. Kami juga dapat mengeksplorasi kelancaran jalur yang dilalui yang sesuai dengan prediksi profil berurutan berdasarkan waktu. Simulasi yang ditampilkan yang memperlihatkan pergeseran perilaku sampel disajikan dalam Gambar 17a ; untuk hasil animasi dan pembahasan lebih lanjut, silakan lihat video tambahan dan Bagian D dari materi tambahan. Ruang MPACT terstruktur bersifat umum karena tidak bergantung pada simulator/generator yang mendasarinya. Untuk inferensi, kami dapat menggunakan skenario ‘tidak diketahui’ (mathematical equation) dari generator eksternal tambahan, yaitu ETH Hotel [ PESVG09 ], CEDRL [ PAC25 ], Lee [ LCHL07 ] dan versi lain dari Zara [ LCL07 ]. Kami menerapkan model MPACT dan memplot prediksi pada Gambar 15. Melakukan pengelompokan K-means pada vektor laten, kami menemukan 5 titik terdekat dan mengklasifikasikan yang tidak diketahuimathematical equationke skenario yang paling mungkin dengan menggunakan suara mayoritas (contoh ditunjukkan pada Gambar 17b–d ).
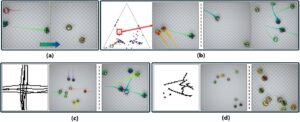
Kita juga dapat melakukan operasi matematika di ruang laten, seperti pada Gambar 16. Misalnya, dengan dua contoh skenario, pengguna dapat menerapkan interpolasi linier di antara keduanya untuk membuat perilaku campuran antara, yang dikontrol oleh skenario yang diketahui pengguna dan secara implisit menentukan tugas kerumunan yang diinginkan.
4.4 Studi Eksperimental
4.4.1 Studi pengguna
Pengaturan:
Kami melakukan studi pengguna selama 20 menit dengan 44 peserta untuk menilai kualitas dan kredibilitas simulasi kerangka kerja kami. Peserta kami beragam dalam hal usia (18, 65), jenis kelamin (25M/17F), dan negara tempat bekerja. Pengguna diminta untuk menyelesaikan studi di komputer desktop. Secara keseluruhan, pengetahuan simulasi kerumunan pengguna bervariasi dengan rata-ratamathematical equation; kami yakin ini merupakan skor yang relatif tinggi untuk studi tanpa prasyarat. Melalui studi ini, kami bertujuan untuk menguji sejauh mana perilaku yang dihasilkan oleh MPACT tampak realistis bagi pengguna. Untuk melakukannya, kami menampilkan 10 video simulasi nyata dan MPACT secara acak, meminta peserta untuk memilih yang lebih realistis. Peserta diminta untuk menonton video secara penuh dan menilai berdasarkan perilaku keseluruhan, bukan jalur per bingkai, dan kami mengumpulkan respons mereka.
Temuan:
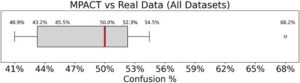
Kami mengukur seberapa bingungnya pengguna ketika harus membedakan jalur nyata versus jalur MPACT dan merangkum hasilnya pada Gambar 18. Kita dapat menyimpulkan bahwa sekitar setengah dari waktu pengguna tidak dapat membedakan jalur nyata. Khususnya, kebingungan ini bukan karena merata-ratakan jawaban yang hampir benar dan hampir salah di seluruh sampel. Sebaliknya, berdasarkan per sampel, pengguna sama-sama bingung sekitarmathematical equationdari kasus-kasus tersebut. Misalnya, pada contoh 2, sekitarmathematical equationpengguna salah mengidentifikasi jalur yang ditampilkan sebagai ‘nyata’ padahal, sebenarnya, jalur tersebut dibuat oleh MPACT. Kebingungan yang konsisten di seluruh sampel ini menunjukkan bahwa pengguna kesulitan membedakan antara jalur nyata dan jalur MPACT. Analisis tambahan dapat ditemukan di Bagian E dari materi tambahan.
4.4.2 Studi ahli
Pengaturan:
Kami melakukan eksperimen tambahan, dengan merancang studi yang secara langsung membandingkan prediksi MPACT dengan garis dasar CCP, sebagaimana ditetapkan oleh “para pakar” (enam pengguna terlatih dengan pengetahuan luas tentang simulasi kerumunan). Kami meminta para pakar untuk secara manual menghasilkan serangkaian profil perilaku yang cocok dengan video input. Upaya kami adalah untuk mendapatkan padanan manual dari perilaku otomatis yang kami prediksi MPACT, dan membandingkannya dalam hal kinerja dan kualitas. Temuan studi ini memberikan wawasan tentang kegunaan praktis model kami, karena kami menilai seberapa mudah tugas ini dapat diselesaikan dengan melewati metode optimasi otomatis, tetapi sebaliknya, memiliki pengguna yang mampu secara langsung menentukan nilai parameter, berdasarkan pengalaman. Selama studi pakar ini, pengguna pertama-tama menyelesaikan eksperimen ‘demo’ untuk membiasakan diri dengan antarmuka; tidak ada data yang direkam selama fase ini. Kemudian, studi resmi dimulai yang terdiri dari tiga tahap, sebagaimana dijelaskan dalam Bagian 4.3 .
Temuan Efisiensi Waktu:
Karena metode kami otomatis, satu keuntungan yang kami harapkan dibanding alternatif manual adalah kecepatan inferensi. Memang, setelah mencatat waktu yang dihabiskan untuk menentukan bobot yang dipilih, kami dapat memverifikasi bahwa para ahli membutuhkan waktu lebih lama daripada metode kami, dengan rata-rata 9,71 menit versus 10,2 detik.
Temuan Berkualitas:
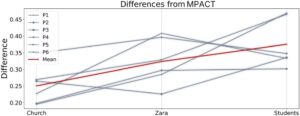
Untuk mendapatkan gambaran tentang seberapa dekat bobot pakar dengan bobot yang diprediksi (MPACT), kami memetakan perbedaan rata-rata MPACT dengan setiap partisipan, yang menunjukkan tren peningkatan secara keseluruhan (Gambar 19 ). Dalam kumpulan data yang kurang kompleks seperti Church, partisipan dapat mencocokkan MPACT dengan lebih mudah, namun, kualitas replikasi menurun dengan meningkatnya kompleksitas perilaku, seperti yang terlihat dalam kumpulan data Students. Dengan demikian, bahkan pengguna ahli menunjukkan penyimpangan yang signifikan ketika mencoba mereplikasi perilaku yang dimaksudkan dalam skenario yang kompleks. Oleh karena itu, memiliki metode yang otomatis dan stabil bermanfaat, selama lebih dekat dengan data sebenarnya daripada alternatifnya. Hasil lebih lanjut dapat ditemukan di materi tambahan Bagian F.
Untuk menilai kesamaan dengan data riil, kami membangun FD dari jalur yang diambil dari data riil, pakar, dan MPACT (Gambar 20 ), untuk masing-masing dari tiga set data. Kami mengamati bahwa lari riil, MPACT, dan sebagian besar partisipan mengikuti pola yang diharapkan: arus kerumunan meningkat dengan kepadatan hingga kepadatan tinggi mengurangi kecepatan agen, yang menyiratkan generasi yang masuk akal. Dalam menentukan mana yang lebih dekat dengan kurva data riil, kami melihat bahwa kurva MPACT adalah yang paling konsisten serupa. Misalnya, di Zara, kami melihat bahwa P2 juga berhasil menangkap perilaku kerumunan riil, tetapi gagal melakukannya di dua set data lainnya. Bahkan dibandingkan dengan P5 (partisipan paling sukses), MPACT masih lebih dekat dengan kurva riil setidaknya di set data Zara.

5 Pembahasan, Kesimpulan dan Arah Masa Depan
Kesimpulannya, makalah ini menyajikan kerangka kerja MPACT , model prediksi berbasis gambar yang mengekstrak nilai bobot optimal dari lintasan input yang tidak berlabel, untuk parameter khusus simulator. Alur kerja MPACT memetakan tugas-tugas kerumunan yang kompleks dan saling terkait ke profil yang ringkas dan dapat dijelaskan, yang memungkinkan parameterisasi perilaku di alam liar. Profil-profil ini menangkap perilaku dalam data input dan dapat diterapkan ke simulator kerumunan (‘modCCP’) untuk mencerminkannya dalam simulasi yang dihasilkan. Selain itu, pekerjaan kami tidak terbatas pada parameter tipe navigasi, tetapi beroperasi dalam ruang parameter yang rumit; ini mencakup beragam perilaku dari yang sederhana misalnya, hanya mencari tujuan, hingga yang tingkat lanjut seperti campuran tujuan, pengelompokan, dan interaksi dengan POI.
Kegunaan kerangka kerja dibuka melalui UI MPACT di mana pengguna mengambil alih kendali dan pembuatan dengan memanfaatkan prediksi MPACT. Pengguna secara implisit mendefinisikan pola perilaku yang diinginkan dengan memilih skenario kerumunan masukan yang sesuai, kemudian mewujudkan perilaku referensi ini dengan menerapkan profil yang diprediksi MPACT. Profil ini dapat didistribusikan dalam ruang dan waktu sesuai keinginan mereka, dalam lingkungan virtual khusus, tanpa mengorbankan kemungkinan simulasi. Beberapa pengenalan dengan antarmuka dan bagaimana parameter berkorelasi dengan pergerakan agen diperlukan untuk pemanfaatan kerangka kerja yang tepat, misalnya, seperti apa profil setengah pengelompokan dan setengah tujuan.
Kami melakukan serangkaian eksperimen dengan memperhatikan representasi masukan kami (pengodean berbasis gambar) dan ruang laten MPACT. Temuan kami menunjukkan bahwa MPACT secara efektif mengabstraksikan data kerumunan menjadi representasi padat yang mengodekan kesamaan perilaku, yang juga kompatibel dengan model pembuatan profil yang menetapkan profil perilaku yang dapat dijelaskan dan dikendalikan ke data kerumunan yang tidak diberi label. Kami mengevaluasi kualitas pembuatan model kami secara kualitatif dan kuantitatif, menetapkan MPACT sebagai kerangka kerja yang cepat dan andal untuk menghasilkan simulasi yang masuk akal. Perbandingan kuantitatif dari distribusi metrik yang terkait dengan kerumunan dan yang mencirikan perilaku (misalnya, kepadatan) terhadap metode yang ada dan data nyata, mensubsidi kontribusi MPACT.
Meskipun kerangka kerja kami memiliki kelebihan dan efektivitas, kerangka kerja ini memiliki keterbatasan tertentu. Saat ini, kami tidak mengintegrasikan metode video-ke-lintasan, sehingga hanya data kerumunan yang dilacak yang dapat digunakan tanpa praproses. Selain itu, kami mengakui bahwa model kerumunan yang mendasarinya yang kami gunakan, memiliki keterbatasannya sendiri yang dapat terakumulasi dalam kerangka kerja kami misalnya, CCP belum dilatih pada data dunia nyata. Paradigma MPACT berpotensi untuk diperluas ke simulator lain, yang memerlukan pengaturan kerangka kerja yang serupa tetapi pelatihan ulang dengan konfigurasi dan data yang berbeda. Secara umum, pelatihan dengan data nyata sangat menantang karena kurangnya pasangan lintasan-parameter. Arah yang mungkin adalah meminta para ahli untuk memberi label perilaku dominan, yang memungkinkan penyempurnaan alur kerja yang diusulkan. Akhirnya, kami menyadari bahwa peningkatan lebih lanjut pada UI dapat dilakukan untuk efektivitas maksimum seperti memungkinkan penyebaran profil yang dipilih di jendela waktu mendatang, dan mengintegrasikan prediksi lintasan dengan mulus.
Pendekatan kami membuka kemungkinan baru untuk menyempurnakan dan memperluas kerangka kerja MPACT. Peningkatan yang menarik pada metode kami adalah memprediksi distribusi profil untuk setiap area, alih-alih satu saja, tambahan yang juga akan sangat meningkatkan kompleksitas. Selain itu, sistem kami saat ini memperlakukan area perilaku sebagai segmen persegi panjang berukuran tetap dan diskritisasi area tidak universal di seluruh data masukan yang berbeda. Di masa mendatang, kami bertujuan untuk mengeksplorasi pengintegrasian bentuk area yang lebih kompleks dan mengotomatiskan pembentukannya berdasarkan informasi lingkungan nyata yang diamati. Studi masa depan yang menjanjikan adalah memperluas rentang parameter yang dapat dijelaskan dengan memperkenalkan versi modCCP yang disempurnakan; namun, semakin banyak bobot (perilaku) yang kami tambahkan, semakin menantang untuk menyeimbangkannya. Untuk mempertahankan sejumlah kecil bobot per kebijakan, salah satu pilihannya adalah memiliki kebijakan terpisah untuk set bobot yang berbeda.
Generalisasi metode kami, serta penerapannya pada skenario dunia nyata, dapat ditingkatkan. Pembelajaran transfer dapat dieksplorasi untuk menerjemahkan profil modCCP menjadi parameter simulator kerumunan lainnya. Yang lebih penting, melihat distribusi skenario nyata dalam ruang laten MPACT (Gambar 15 ), kami melihat manifold yang lebih kecil dalam data nyata daripada ruang pelatihan. Ini menantang keberadaan definisi bobot interaksi saat ini dalam perilaku nyata. Kami bertujuan untuk menyelidiki lebih lanjut formalisasi beberapa jenis perilaku dan menyesuaikan data pelatihan kami agar lebih selaras dengan ‘ruang data nyata’. Ini menciptakan peluang untuk sintesis kerumunan yang kreatif dan terinformasi. Namun, kami menekankan bahwa ini menantang karena memerlukan penelitian ekstensif dan analisis yang cermat untuk mencapai hasil yang tidak bias.
